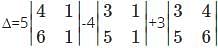Mathematics: CUET Mock Test - 6 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 6
What will be the value of x + y + z if cos-1 x + cos-1 y + cos-1 z = 3π?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the order of the matrix is m×n, then how many elements will there be in the matrix?
The matrix which follows the conditions m=n is called?
Which of the following matrices will not have a determinant?
Which of the following is a matrix of the order 2×2 where the equation of the elements is given by aij =i+j.
Consider the matrix A= 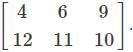 What is the type of matrix?
What is the type of matrix?
Which of the following relations is symmetric but neither reflexive nor transitive for a set A = {1, 2, 3}.
What is the value of sin-1(-x) for all x belongs to [-1, 1]?
Which of the following relations is transitive but not reflexive for the set S={3, 4, 6}?
What is the value of r = 1Σn f(x) if f(r) = 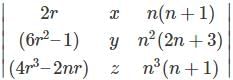 where n € N?
where n € N?
The matrix which follows the condition m>n is called as _______
Let R be a relation in the set N given by R={(a,b): a+b=5, b>1}. Which of the following will satisfy the given relation?
What is the value of cos-1(-x) for all x belongs to [-1, 1]?
Which one is correct, the following system of linear equations 2x – 3y + 4z = 7, 3x – 4y + 5z = 8, 4x – 5y + 6z = 9 has?
Which of the following relations is reflexive but not transitive for the set T = {7, 8, 9}?
Which of the following is not a possible ordered pair for a matrix with 6 elements.
|
8 docs|148 tests
|


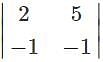 .
.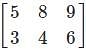 is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.
is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.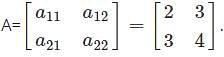
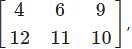 m = 3 and n = 2 i.e.
m = 3 and n = 2 i.e.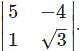
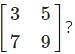
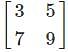 is 2. Therefore, the order of the matrix is 2×2(m×n).
is 2. Therefore, the order of the matrix is 2×2(m×n). is ____
is ____ is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.
is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.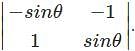
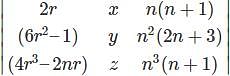
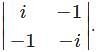
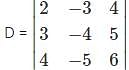
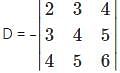
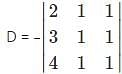
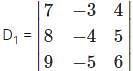
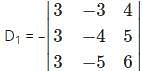
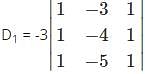
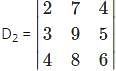
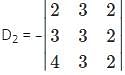
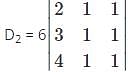
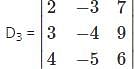
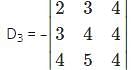
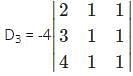
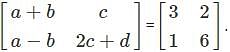
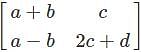 and
and 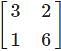 are equal matrices. Comparing the two matrices, we get a-b=3, c=2, a-b=1, 2c+d=6
are equal matrices. Comparing the two matrices, we get a-b=3, c=2, a-b=1, 2c+d=6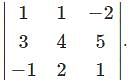
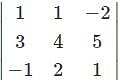
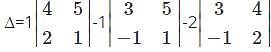
 is a diagonal matrix.
is a diagonal matrix. .
.