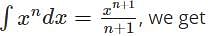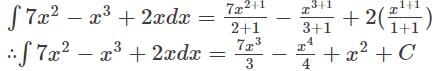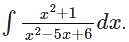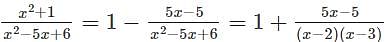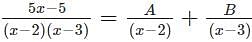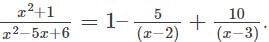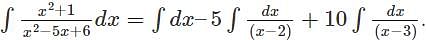Mathematics: CUET Mock Test - 9 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 9
Find the values of x and y for the given system of equations.
3x-2y=3
2x+2y=4
3x-2y=3
2x+2y=4
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The total cost N(x) in rupees, associated with the production of x units of an item is given by N(x)=0.06x3-0.01x2+10x-43. Find the marginal cost when 5 units are produced.
The cost of 8kg apple and 3kg is Rs 70. The cost of 10kg apple and 6kg orange is 90. Find the cost of each item if x is the cost of apples per kg and y is the cost of oranges per kg.
The length of the rectangle is changing at a rate of 4 cm/s and the area is changing at the rate of 8 cm/s. What will be the rate of change of width if the length is 4cm and the width is 1 cm.
For a given system of equations if |A|=0 and (adj A)B≠O(zero matrix), then which of the following is correct regarding the solutions of the given equations?
Find the second order derivative of y=3x2 1 + log(4x)
For which of the values of x, the rate of increase of the function y=3x2-2x+7 is 4 times the rate of increase of x?
Find the value of x and y for the given system of equations.
3x+4y=6
5x-4y=4
The volume of a cube of edge x is increasing at a rate of 12 cm/s. Find the rate of change of edge of the cube when the edge is 6 cm.
What is the slope of the tangent to the curve y = 2x/(x2 + 1) at (0, 0)?
The value of f’(x) is -1 at the point P on a continuous curve y = f(x). What is the angle which the tangent to the curve at P makes with the positive direction of x axis?
|
8 docs|148 tests
|


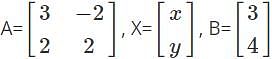
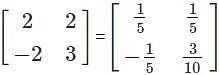

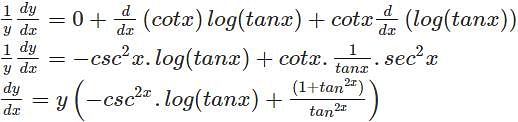
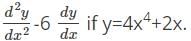
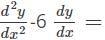 48x2−96x3−12
48x2−96x3−12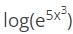 w.r.t x.
w.r.t x.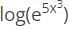
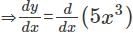
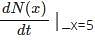 = 0.18(5)2-0.02(5)+10
= 0.18(5)2-0.02(5)+10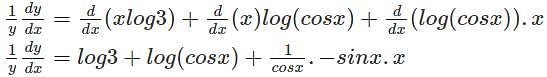
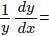 log3+log(cosx)-x tanx
log3+log(cosx)-x tanx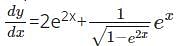
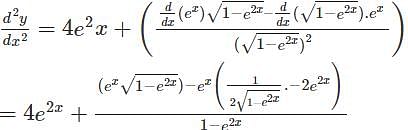
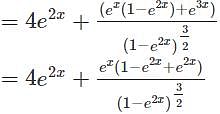
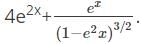
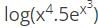 w.r.t x.
w.r.t x.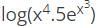
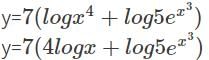
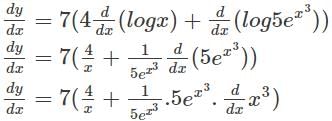
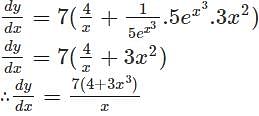
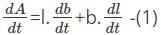
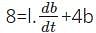
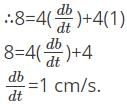
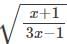 with respect to x.
with respect to x.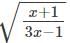
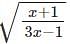
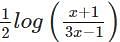
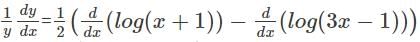
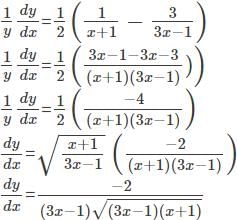
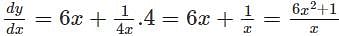


 logx w.r.t x.
logx w.r.t x.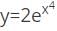 logx
logx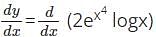
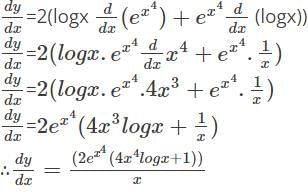
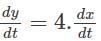

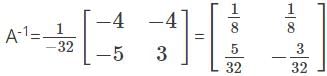

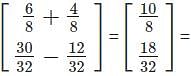

 with respect to x.
with respect to x.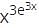
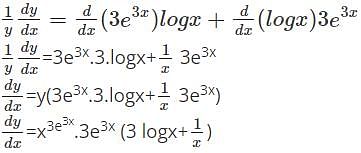

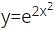
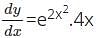
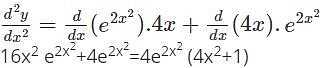
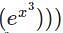 w.r.t x.
w.r.t x.
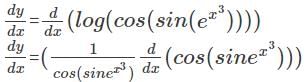
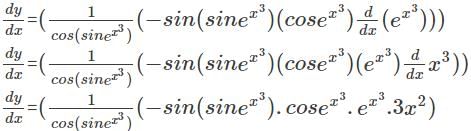


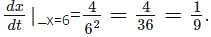
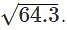
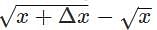
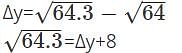
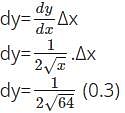
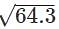 is 8+0.01875=8.01875
is 8+0.01875=8.01875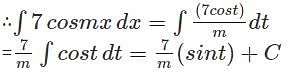
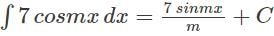
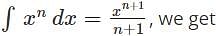

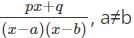 represents?
represents?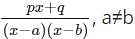 can also be written as
can also be written as 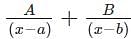 and is further used to solve integration by partial fractions numerical.
and is further used to solve integration by partial fractions numerical.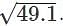
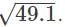 Let x=49 and Δx=0.1
Let x=49 and Δx=0.1
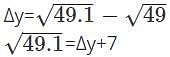
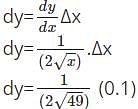
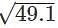 is 7+0.00714=7.00714
is 7+0.00714=7.00714