Important Questions Test: Mensuration
20 Questions MCQ Test Mathematics (Maths) Class 6 | Important Questions Test: Mensuration
| 1 Crore+ students have signed up on EduRev. Have you? |
The perimeter of a square is 100 cm. Its side is
If the perimeter of a square is 44 cm, then its area is
If the perimeter of a square is 16 cm, then its area is
The side of a square is 8 cm. If its side is doubled, then its new perimeter is
The length and breadth of a rectangle are 10 cm and 8 cm respectively. If its length is doubled, then its new area is
Side of Square = a2
(7)2
= 49 m2
__________ is the distance covered along the boundary forming a closed figure when you go round the figure once.
Perimeter of a square = ________ × length of a side
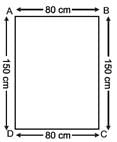
Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?
Let ABCD is a park whose lengths are BC, AD and widths are AB, CD, respectively. Hence, AB = CD = 80 m. and BC = DA = 150m Now, the sum of the lengths of four sides
=AB + BC + CD + DA
= 80 m + 150 m + 80 m + 150 m
= (80 + 150 + 80 + 150) m
=460 m
Perimeter of the park = sum of the lengths of four sides of the park = 460 m
Hence, distance covered by Meera is 460 m.
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Find the area of square whose perimeter is 48cm
Find the perimeter of a regular pentagon with each side measuring 3 cm.
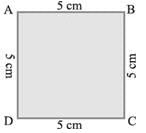
What is the perimeter of the following figure ?
Find the perimeter of an isosceles triangle with equal sides 8 cm each and third side 6 cm.
Perimeter of a rectangle = _________ × (length + breadth)
Perimeter of an __________ = 3 × length of a side
A farmer has a rectangular field of length and breadth 240 m and 180 m respectively. He wants to fence it with 3 rounds of rope. What is the total length of rope he must use?
If the area of rectangle increases from 2 cm2 to 4 cm2 the perimeter will
Which figure encloses more area: a square of side 2 cm ; a rectangle of side 3 cm and 2 cm ;An equilateral triangle of side 4 cm?
|
167 videos|275 docs|43 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
167 videos|275 docs|43 tests
|
Download free EduRev App
Related content with Important Questions Test: Mensuration
|
|
|
|
Related tests with Important Questions Test: Mensuration
|
|
|
|
|
|
© EduRev
|
Follow Us
|