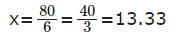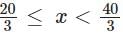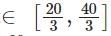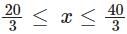Test: Linear Equations- 1 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Linear Equations- 1
The number of solutions of the equation 2x + y = 40 where both x and y are positive integers and x <= y is:
For a real number x the condition |3x - 20| + |3x - 40| = 20 necessarily holds if
The number of integers n that satisfy the inequalities | n - 60| < n - 100| < |n - 20| is
Consider the equation:
|x-5|2 + 5 |x - 5| - 24 = 0
The sum of all the real roots of the above equationis:
Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
If 2 ≤ |x – 1| × |y + 3| ≤ 5 and both x and y are negative integers, find the number of possible combinations of x and y.
The minimum possible value of the sum of the squares of the roots of the equation x2 + (a + 3) x - (a + 5) = 0 is
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc – (a + b + c)]?
|
191 videos|133 docs|110 tests
|