Test: Mensuration- 2 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Mensuration- 2
A right circular cone has height H and radius R. A small cone is cut off at the top by a plane parallel to the base. At what height above the base the section has been made?
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15
A sphere of radius r is cut by a plane at a distance of h from its center, thereby breaking this sphere into two different pieces. The cumulative surface area of these two pieces is 25% more than that of the sphere. Find h.
Two mutually perpendicular chords AB and CD meet at a point P inside the circle such that AP = 6 cms, PB = 4 units and DP = 3 units. What is the area of the circle?
Cylindrical cans of cricket balls are to be packed in a box. Each can has a radius of 7 cm and height of 30 cm. Dimension of the box is l = 76 cm, b = 46 cm, h = 45 cm. What is the maximum number of cans that can fit in the box?
PQRS is a square of sides 2 cm & ST = 2 cm. Also, PT=RT. What is the area of ?PST?
A string is wound around two circular disk as shown. If the radius of the two disk are 40 cm and 30 cm respectively. What is the total length of the string?
Figure above shows a box which has to be completely wrapped with paper. However, a single Sheet of paper need to be used without any tearing. The dimension of the required paper could be
An inverted right circular cone has a radius of 9 cm. This cone is partly filled with oil which is dipping from a hole in the tip at a rate of 1cm2/hour. Currently the level of oil 3 cm from top and surface area is 36π cm2. How long will it take the cone to be completely empty?
A square PQRS has an equilateral triangle PTO inscribed as shown:
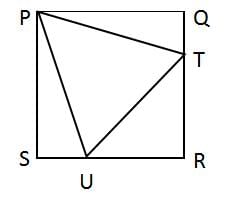
What is the ratio of AΔPQT to AΔTRU?
A spherical shaped sweet is placed inside a cube of side 5 cm such that the sweet just fits the cube. A fly is sitting on one of the vertices of the cube. What is the shortest distance the fly must travel to reach the sweet?
|
191 videos|133 docs|110 tests
|



















