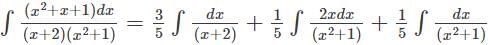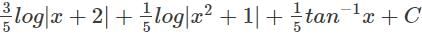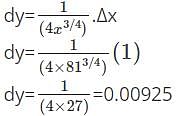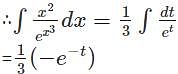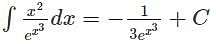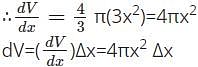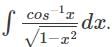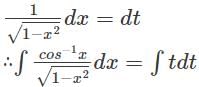Mathematics: CUET Mock Test - 10 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 10
What will be the average rate of change of the function [y = 16 – x2] between x = 3 and x = 4?
What will be the approximate change in the surface area of a cube of side xm caused by increasing the side by 2%.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What will be the average rate of change of the function [y = 16 – x2] at x = 4?
Find the approximate value of f(4.04), where f(x)=7x3+6x2-4x+3.
What will be the value of the co-ordinate whose position of a particle moving along the parabola y2 = 4x at which the rate at of increase of the abscissa is twice the rate of increase of the ordinate?
The time rate of change of the radius of a sphere is 1/2π. When it’s radius is 5cm, what will be the rate of change of the surface of the sphere with time?
Find the approximate change in the volume of cube of side xm caused by increasing the side by 6%.
A solid cube changes its volume such that its shape remains unchanged. For such a cube of unit volume, what will be the value of rate of change of volume?
A 5 ft long man walks away from the foot of a 12(½) ft high lamp post at the rate of 3 mph. What will be the rate at which the shadow increases?
Find the approximate error in the volume of the sphere if the radius of the sphere is measured to be 6cm with an error of 0.07cm.
For the given equation (x+2) (x+4) = x2 + 6x + 8, how many values of x satisfies this equation?
|
8 docs|148 tests
|


 .
.
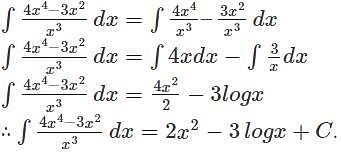
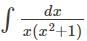 equals ______
equals ______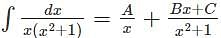
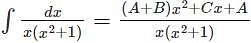
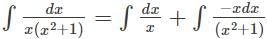
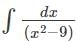 equals ___
equals ___
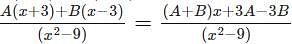
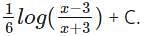
 .
.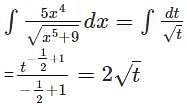
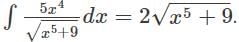
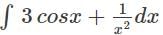
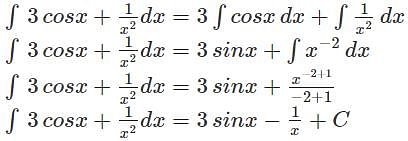
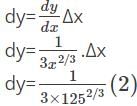
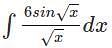
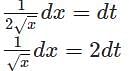
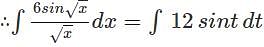
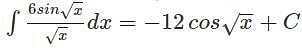
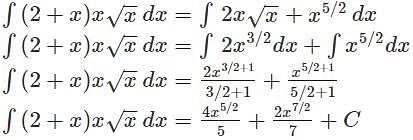
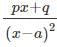 represents?
represents?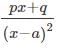 which can also be written as
which can also be written as 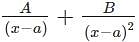 and is further used to solve integration by partial fractions numerical.
and is further used to solve integration by partial fractions numerical.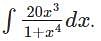
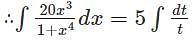
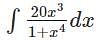 = 5log(1+x4)+C
= 5log(1+x4)+C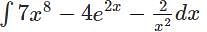
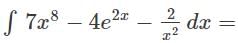
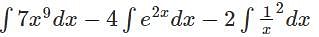
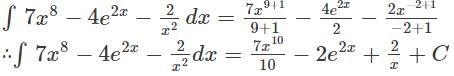
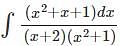 equals ______
equals ______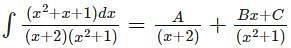
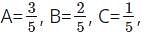 now putting these values in the equation we get,
now putting these values in the equation we get,