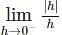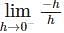Mathematics: CUET Mock Test - 2 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 2
A particle moves in a straight-line OA; the distance of the particle from O at time t seconds is x ft, where x = a + bt + ct2 (a, b > 0). What will be the nature of motion of the particle when c = 0?
A particle moving in a straight line traverses a distance x in time t. If t = x2/2 + x, then which one is correct?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds, respectively.What is the velocity of the particle in 3 seconds?
The distance x of a particle moving along a straight line from a fixed point on the line at time t after start is given by t = ax2 + bx + c (a, b, c are positive constants). If v be the velocity of the particle and u(≠0) be the initial velocity of the particle then which one is correct?
A particle moves in a straight line and its velocity v at time t seconds is given byv = 3t2 – 4t + 5 cm/second. What will be the distance travelled by the particle during first 3 seconds after the start?
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds,respectively.What is the distance described by the particle in 3 seconds?
A particle moves in a horizontal straight line under retardation kv3, where v is the velocity at time t and k is a positive constant. If initial velocity be u and x be the displacement at time,then which one is correct?
The distance s of a particle moving along a straight line from a fixed-pointO on the line at time t seconds after start is given by x = (t – 1)2(t – 2)2. What will be the distance of the particle from O when its velocity is zero?
What will be the nature of the equation sin(x + α)/sin(x + β)?
Given, f(x) = x3 – 12x2 + 45x + 8. What is the maximum value of f(x)?
Given, f(x) = x3 – 12x2 + 45x + 8. What is the minimum value of f(x)?
A particle is moving in a straight line and its distance x from a fixed point on the line at any time t seconds is given by, x = t4/12 – 2t3/3 + 3t2/2 + t + 15. At what time is the velocity minimum?
Given, f(x) = x3 – 12x2 + 45x + 8. At which point does f(x) has its maximum?
Given, f(x) = x3 – 12x2 + 45x + 8. At which point does f(x) has its minimum?
At which point does f(x) = |x – 1| has itslocal minimum?
A particle is moving in a straight line and its distance x from a fixed point on the line at any time t seconds is given by, x = t4/12 – 2t3/3 + 3t2/2 + t + 15. What is the minimum velocity?
What will be the equation of the normal to the parabola y2 = 5x that makes an angle 45° with the x axis?
What will be the equation of the normal to the parabola y2 = 3x which is perpendicular to the line y = 2x + 4?
What will be the length of a tangent from the point (7, 2) to the circle 2x2 + 2y2 + 5 x + y = 15?
What will be the equation of the circle which touches the line x + 2y + 5 = 0 and passes through the point of intersection of the circle x2 + y2 = 1 and x2 + y2 + 2x + 4y + 1 = 0?
If the curves x2/a + y2/b = 1 and x2/c + y2/d = 1 intersect at right angles, then which one is the correct relation?
What will be the co-ordinates of the foot of the normal to the parabola y2 = 5x that makes an angle 45° with the x axis?
What will be the co-ordinates of the foot of the normal to the parabola y2 = 3x which is perpendicular to the line y = 2x + 4?
If the normal to the ellipse x2 + 3y2 = 12 at the point be inclined at 60° to the major axis, then at what angle does the line joining the curve to the point is inclined to the same axis?
What will be the value of angle between the curves x2 - y2 = 2a2 and xv + y2 = 4a2?
(a1, a2) ∈R implies that (a2, a1) ∈ R, for all a1, a2∈A. This condition is for which of the following relations?
Bernoulli trials are also called as _____ or _____ questions.
|
8 docs|148 tests
|


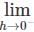 − hf(c + h) – f(c)
− hf(c + h) – f(c)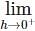 + hf(c + h) – f(c) are finite and equal.
+ hf(c + h) – f(c) are finite and equal.