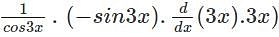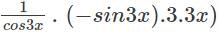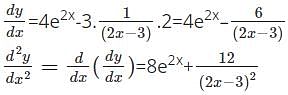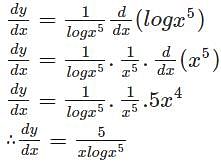Mathematics: CUET Mock Test - 8 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 8
If f(x) = 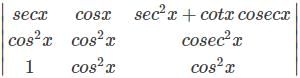 then what is the value of 0∫π/2 f(x) dx =
then what is the value of 0∫π/2 f(x) dx =
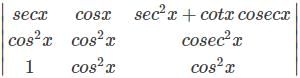 then what is the value of 0∫π/2 f(x) dx =
then what is the value of 0∫π/2 f(x) dx = | 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the area of the triangle with the vertices (2,3), (4,1), (5,0).
For which of the elements in the determinant Δ= 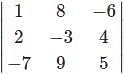 the cofactor is -37.
the cofactor is -37.
What is the relation between the two determinants f(x) = 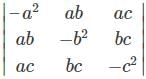 and g(x) =
and g(x) = 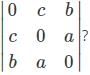
Find the equation of the line joining A(5,1), B(4,0) using determinants.
For which of the following elements in the determinant Δ= 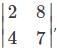 the minor of the element is 2?
the minor of the element is 2?
Find the value of k for which the points (3, 2), (1, 2), (5, k) are collinear.
For which of the following element in the determinant Δ= 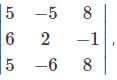 the minor and the cofactor both are zero.
the minor and the cofactor both are zero.
Which of the following conditions holds true for a system of equations to be consistent?
If the rate of change of radius of a circle is 6 cm/s then find the rate of change of area of the circle when r=2 cm.
A given systems of equations is said to be inconsistent if _____
The edge of a cube is increasing at a rate of 7 cm/s. Find the rate of change of area of the cube when x=6 cm.
Find the value of x and y for the given system of equations.
3x+2y=6
5x+y=2
The rate of change of area of a square is 40 cm2/s. What will be the rate of change of side if the side is 10 cm.
Find the second order derivative of y=2e2x-3 log(2x-3).
|
8 docs|148 tests
|


 = 0?
= 0?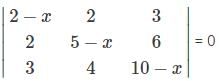
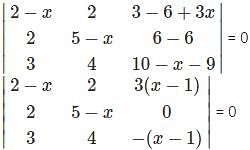
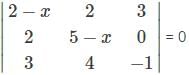
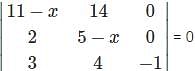

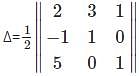
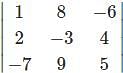
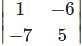 =1(5)-(-6)(-7)=5-42=-37
=1(5)-(-6)(-7)=5-42=-37 .
.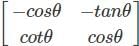
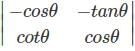
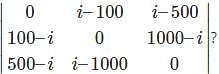
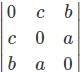
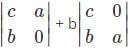
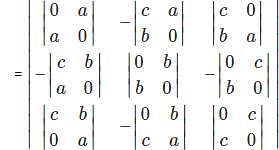
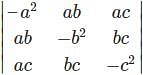
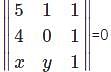
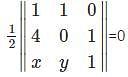
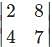

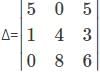
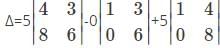
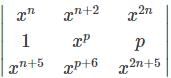 = 0,then what will be the value of p?
= 0,then what will be the value of p?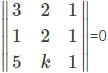
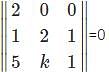
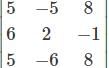
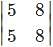 = 40-40 = 0
= 40-40 = 0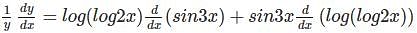
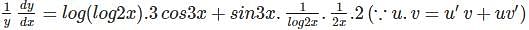
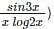
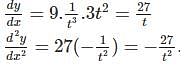
 with respect to x.
with respect to x.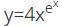
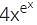
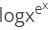 (∵logab =loga+logb)
(∵logab =loga+logb)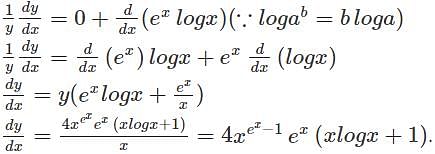
 (sec2x).(2 tanx+3)+ (d/dx) (2 tanx+3).sec2x
(sec2x).(2 tanx+3)+ (d/dx) (2 tanx+3).sec2x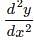 =2 sec2x tanx (2 tanx+3)+sec2x (2 secx tanx)
=2 sec2x tanx (2 tanx+3)+sec2x (2 secx tanx)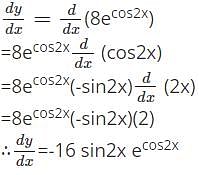
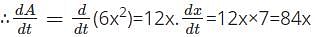
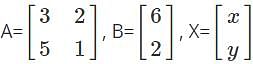

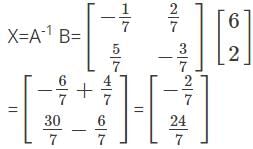
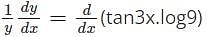
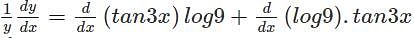 (∵ Using u.v = u′v + uv′)
(∵ Using u.v = u′v + uv′)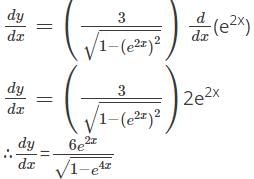
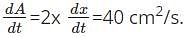
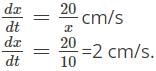
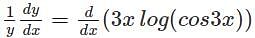
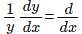 (3x)log(cos3x)+(d/dx)(log(cos3x)).3x
(3x)log(cos3x)+(d/dx)(log(cos3x)).3x (cos3x).3x)
(cos3x).3x)