CAT 2019 Slot 1: LR DI - CAT MCQ
30 Questions MCQ Test - CAT 2019 Slot 1: LR DI
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Q. In how many different ways can the items be arranged on the shelves?
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Q. Which of the following items is not a type of biscuit?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Q. Which of the following can represent the numbers of the empty shelves in a possible arrangement?
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Q. Which of the following statements is necessarily true?
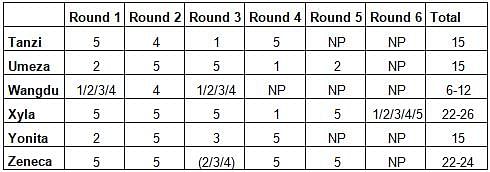
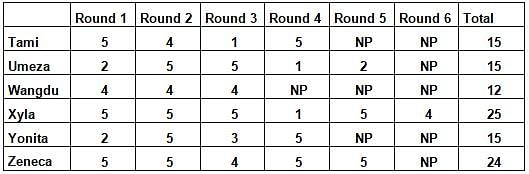
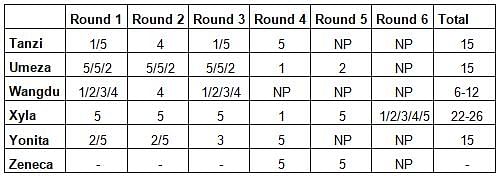
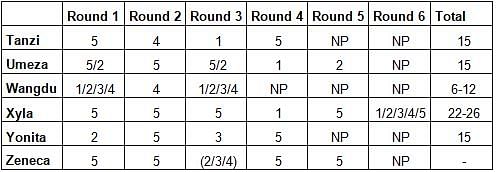
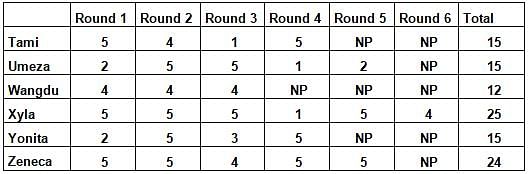
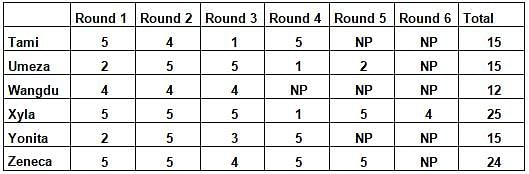
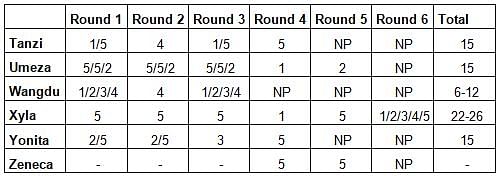
Six players - Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
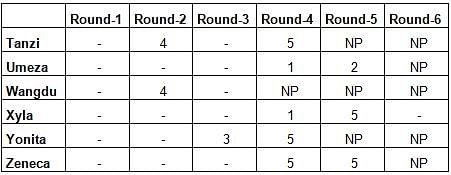
A player’s total score in the tournament was the sum of his/her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
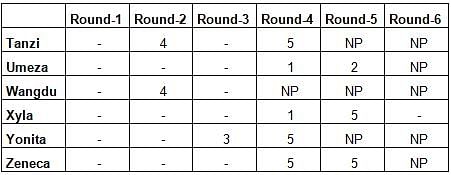
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
Q. What was the highest total score?
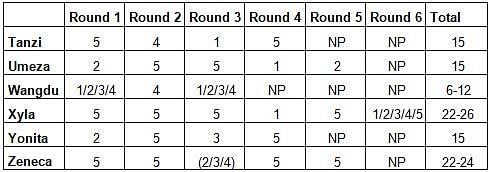
Six players - Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
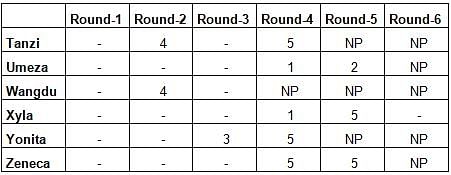
A player’s total score in the tournament was the sum of his/her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
Q. What was Zeneca's total score?
Six players - Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
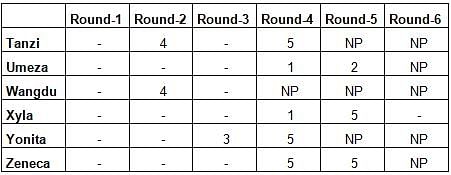
A player’s total score in the tournament was the sum of his/her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
Q. Which of the following statements is true?
Six players - Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
A player’s total score in the tournament was the sum of his/her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
Q. What was Tanzi's score in Round 3?
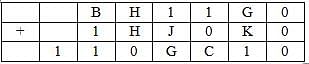
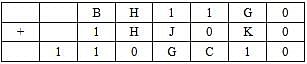
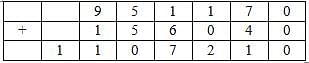
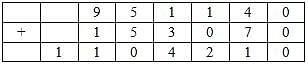
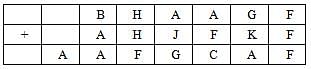
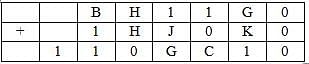
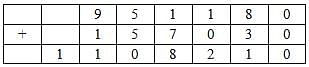
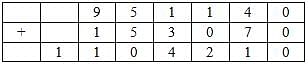
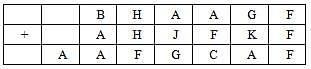
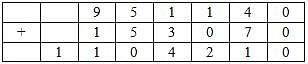
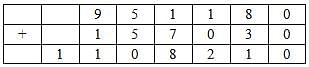
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
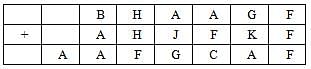
Q. Which digit does the letter A represent?
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
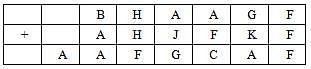
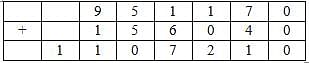
Q. Which digit does the letter B represent?
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
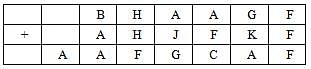
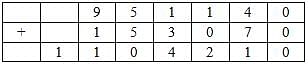
Q. Which among the digits 3, 4, 6 and 7 cannot be represented by the letter D?
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.

Q. Which among the digits 4, 6, 7 and 8 cannot be represented by the letter G?
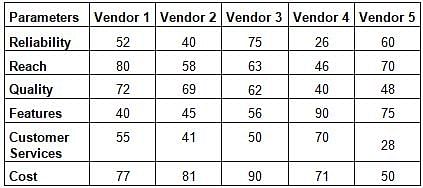
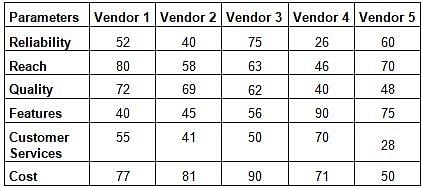
Five vendors are being considered for a service. The evaluation committee evaluated each vendor on six aspects - Cost, Customer Service,Features, Quality, Reach, and Reliability. Each of these evaluations are on a scale of 0 (worst) to 100 (perfect). The evaluation scores on these aspects are shown in the radar chart. For example, Vendor 1 obtains a score of 52 on Reliability, Vendor 2 obtains a score of 45 on Features and Vendor 3 obtains a score of 90 on Cost.
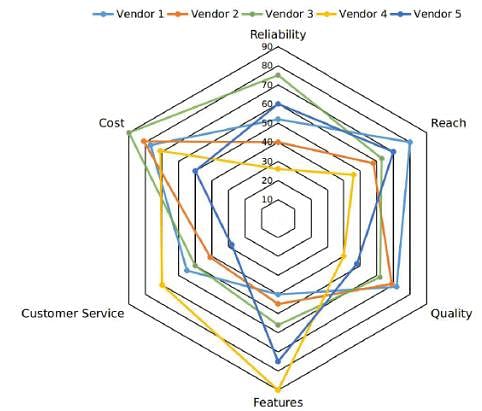
Q. On which aspect is the median score of the five vendors the least?
Five vendors are being considered for a service. The evaluation committee evaluated each vendor on six aspects - Cost, Customer Service, Features, Quality, Reach, and Reliability. Each of these evaluations are on a scale of 0 (worst) to 100 (perfect). The evaluation scores on these aspects are shown in the radar chart. For example, Vendor 1 obtains a score of 52 on Reliability, Vendor 2 obtains a score of 45 on Features and Vendor 3 obtains a score of 90 on Cost.

Q. A vendor's final score is the average of their scores on all six aspects. Which vendor has the highest final score?
Five vendors are being considered for a service. The evaluation committee evaluated each vendor on six aspects - Cost, Customer Service, Features, Quality, Reach, and Reliability. Each of these evaluations are on a scale of 0 (worst) to 100 (perfect). The evaluation scores on these aspects are shown in the radar chart. For example, Vendor 1 obtains a score of 52 on Reliability, Vendor 2 obtains a score of 45 on Features and Vendor 3 obtains a score of 90 on Cost.

Q. List of all the vendors who are among the top two scorers on the maximum number of aspects is:
Five vendors are being considered for a service. The evaluation committee evaluated each vendor on six aspects - Cost, Customer Service, Features, Quality, Reach, and Reliability. Each of these evaluations are on a scale of 0 (worst) to 100 (perfect). The evaluation scores on these aspects are shown in the radar chart. For example, Vendor 1 obtains a score of 52 on Reliability, Vendor 2 obtains a score of 45 on Features and Vendor 3 obtains a score of 90 on Cost.
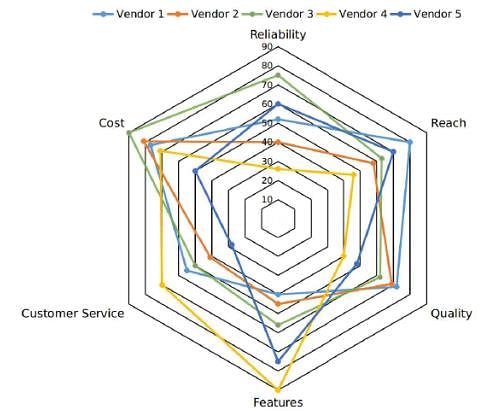
Q. List of all the vendors who are among the top three vendors on all six aspects is:
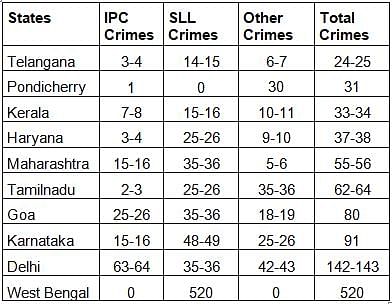
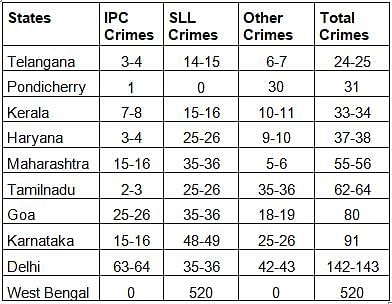
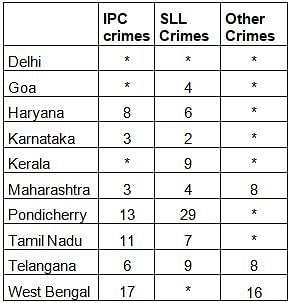
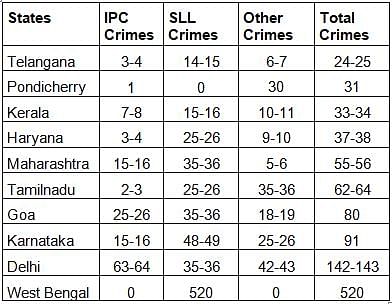
The Ministry of Home Affairs is analysing crimes committed by foreigners in different states and union territories (UT) of India. All cases refer to the ones registered against foreigners in 2016.
The number of cases - classified into three categories: IPC crimes, SLL crimes and other crimes - for nine states/UTs are shown in the figure below. These nine belong to the top ten states/UTs in terms of the total number of cases registered. The remaining state (among top ten) is West Bengal, where all the 520 cases registered were SLL crimes.

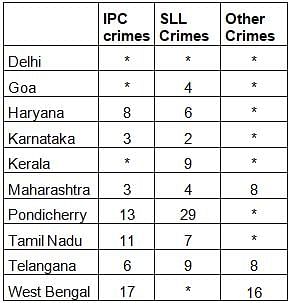
The table below shows the ranks of the ten states/UTs mentioned above among ALL states/UTs of India in terms of the number of cases registered in each of the three category of crimes. A state/UT is given rank r for a category of crimes if there are (r‐1) states/UTs having a larger number of cases registered in that category of crimes. For example, if two states have the same number of cases in a category, and exactly three other states/UTs have larger numbers of cases registered in the same category, then both the states are given rank 4 in that category. Missing ranks in the table are denoted by *.
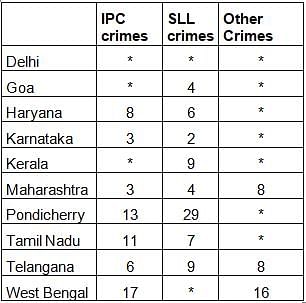
Q. What is the rank of Kerala in the ‘IPC crimes’ category?
The Ministry of Home Affairs is analysing crimes committed by foreigners in different states and union territories (UT) of India. All cases refer to the ones registered against foreigners in 2016.
The number of cases - classified into three categories: IPC crimes, SLL crimes and other crimes - for nine states/UTs are shown in the figure below. These nine belong to the top ten states/UTs in terms of the total number of cases registered. The remaining state (among top ten) is West Bengal, where all the 520 cases registered were SLL crimes.
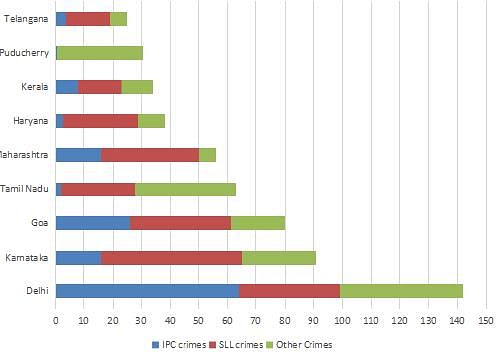
The table below shows the ranks of the ten states/UTs mentioned above among ALL states/UTs of India in terms of the number of cases registered in each of the three category of crimes. A state/UT is given rank r for a category of crimes if there are (r‐1) states/UTs having a larger number of cases registered in that category of crimes. For example, if two states have the same number of cases in a category, and exactly three other states/UTs have larger numbers of cases registered in the same category, then both the states are given rank 4 in that category. Missing ranks in the table are denoted by *.
Q. In the two states where the highest total number of cases are registered, the ratio of the total number of cases in IPC crimes to the total number in SLL crimes is closest to
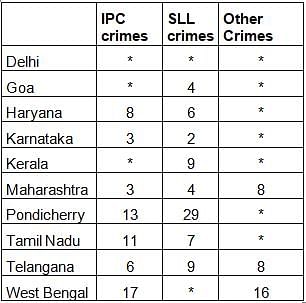
The Ministry of Home Affairs is analysing crimes committed by foreigners in different states and union territories (UT) of India. All cases refer to the ones registered against foreigners in 2016.
The number of cases - classified into three categories: IPC crimes, SLL crimes and other crimes - for nine states/UTs are shown in the figure below. These nine belong to the top ten states/UTs in terms of the total number of cases registered. The remaining state (among top ten) is West Bengal, where all the 520 cases registered were SLL crimes.
The table below shows the ranks of the ten states/UTs mentioned above among ALL states/UTs of India in terms of the number of cases registered in each of the three category of crimes. A state/UT is given rank r for a category of crimes if there are (r‐1) states/UTs having a larger number of cases registered in that category of crimes. For example, if two states have the same number of cases in a category, and exactly three other states/UTs have larger numbers of cases registered in the same category, then both the states are given rank 4 in that category. Missing ranks in the table are denoted by *.
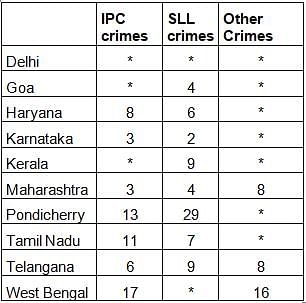
Q. Which of the following is DEFINITELY true about the ranks of states/UT in the ‘other crimes’ category?
i) Tamil Nadu: 2
ii) Pondicherry: 3
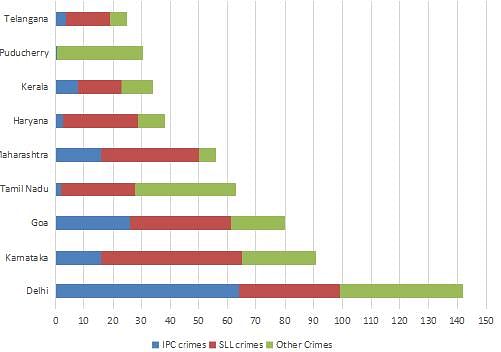
The Ministry of Home Affairs is analysing crimes committed by foreigners in different states and union territories (UT) of India. All cases refer to the ones registered against foreigners in 2016.
The number of cases - classified into three categories: IPC crimes, SLL crimes and other crimes - for nine states/UTs are shown in the figure below. These nine belong to the top ten states/UTs in terms of the total number of cases registered. The remaining state (among top ten) is West Bengal, where all the 520 cases registered were SLL crimes.
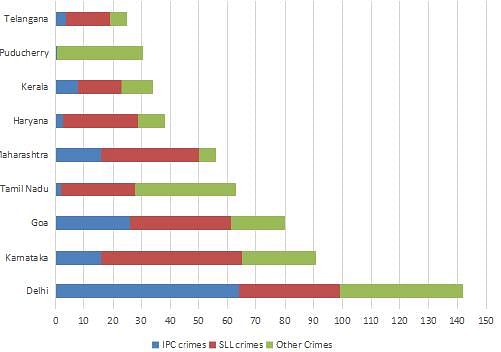
The table below shows the ranks of the ten states/UTs mentioned above among ALL states/UTs of India in terms of the number of cases registered in each of the three category of crimes. A state/UT is given rank r for a category of crimes if there are (r‐1) states/UTs having a larger number of cases registered in that category of crimes. For example, if two states have the same number of cases in a category, and exactly three other states/UTs have larger numbers of cases registered in the same category, then both the states are given rank 4 in that category. Missing ranks in the table are denoted by *.
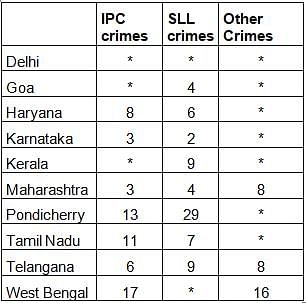
Q. What is the sum of the ranks of Delhi in the three categories of crimes?
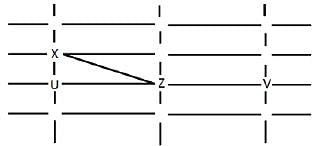
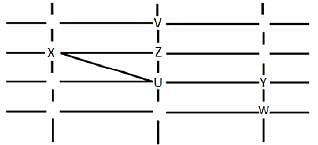
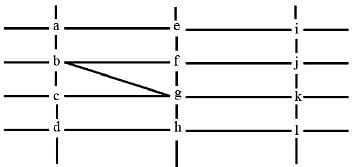
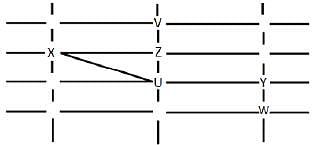
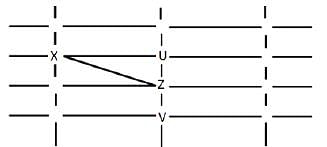
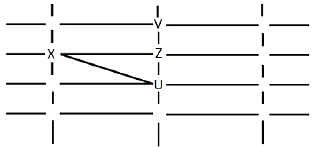
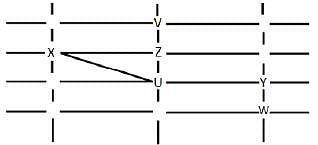
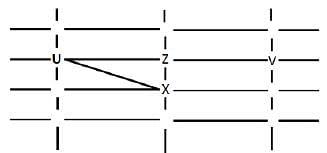
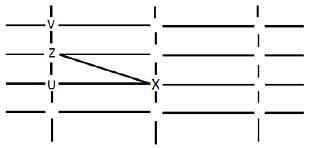
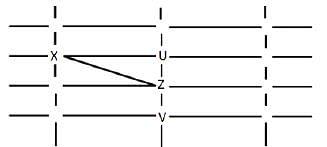
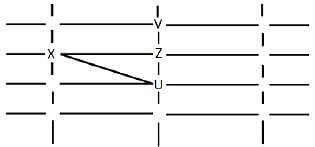
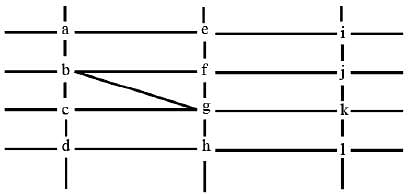
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
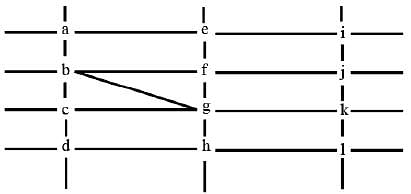
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Q. Who is standing at intersection a?
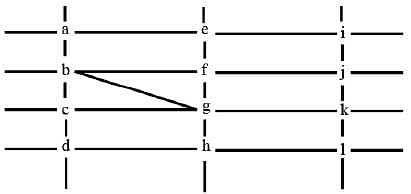
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Q. Who can V see?
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Q. What is the minimum number of street segments that X must cross to reach Y?
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Q. Should a new person stand at intersection d, who among the six would she see?
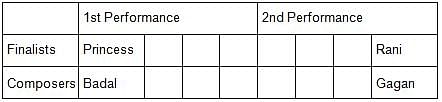
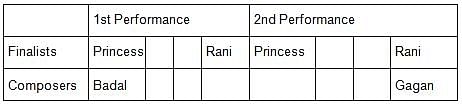
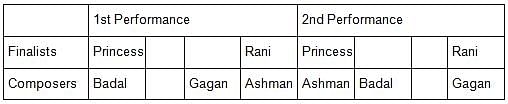
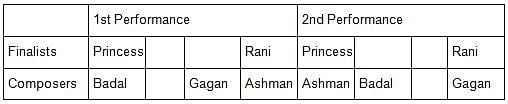
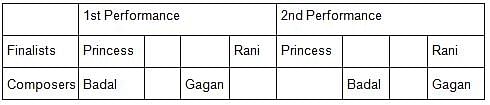
Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Q. Which of the following is true?
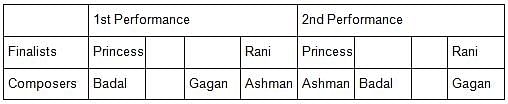
Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Q. Which of the following is FALSE?
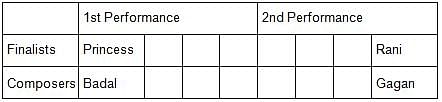
Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Q. The sixth performance was composed by:
Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned item to Princess, assigned any item to Queen.
ii) No composer who assigned item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Q. Which pair of performances were composed by the same composer?
A new game show on TV has 100 boxes numbered 1, 2, . . . , 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, . . . , in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
Q. What is the minimum possible number of different types of prizes?
A new game show on TV has 100 boxes numbered 1, 2, . . . , 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, . . . , in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
Q. What is the maximum possible number of different types of prizes?