Test: Quantitative Reasoning- 3 - CAT MCQ
25 Questions MCQ Test Logical Reasoning (LR) and Data Interpretation (DI) - Test: Quantitative Reasoning- 3
A student got twice as many sums wrong as he got right. If he attempted 48 sums in all, how many did he solve correctly ?
David gets on the elevator at the 11th floor of a building and rides up at the rate of 57 floors per minute. At the same time, Albert gets on an elevator at the 51st floor of the same building and rides down at the rate of 63 floors per minute. If they continue travelling at these rates, then at which floor will their paths cross ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A, B, C and D play a game of cards. A says to B. "If I give you 8 cards, you will have as many as C has and I shall have 3 less than what C has. Also if I take 8 cards from C, I shall have twice as many as D has." If B and D together have 50 cards, how many cards have A got?
I have a few sweets to be distributed. If I keep 2, 3 or 4 in a pack, I am left with one sweet. If I keep 5 in a pack, I am left with none. What is the minimum number of sweets I have to pack and distribute ?
In a group of cows and hens, the number of legs are 14 more than twice the number of heads. The number of cows is
A father tells his son, "I was of your present age when you were born". If the father is 36 now, how old was the boy five years back ?
A fires 5 shots to B's 3 but A kills only once in 3 shots while B kills once in 2 shots. When B has missed 27 times, A has killed
In a class, 3/5 of the students are girls and rest are boys. If 2/9 of the girls and 1/4 of the boys are absent, what part of the total number of students is present ?
In a family, a couple has a son and a daughter. The age of the father is three times that of his daughter and the age of the son is half of that of his mother. The wife is 9 years younger to her husband and the brother is seven years older than his sister. What is the age of the mother ?
If a 1 mm thick paper is folded so that the area is halved at every fold, then what would be the thickness of the pile after 50 folds ?
Mr. X, a mathematician, defines a number as 'connected with 6 if it is divisible by 6 or if the sum of its digits is 6, or if 6 is one of the digits of the number. Other numbers are all 'not connected with 6'. As per this definition, the number of integers from 1 to 60 (both inclusive) which are not connected with 6 is
Find the number which when added to itself 13 times, gives 112.
First bunch of bananas has (1/4) again as many bananas as a second bunch. If the second bunch has 3 bananas less than the first bunch, then the number of bananas in the first bunch is
Aruna cut a cake into two halves and cuts one half into smaller pieces of equal size. Each of the small pieces is twenty grams in weight. If she has seven pieces of the cake in all with her, how heavy was the original cake ?
A total of 324 coins of 20 paise and 25 paise make a sum of Rs. 71. The number of 25-paise coins is
A player holds 13 cards of four suits, of which seven are black and six are red. There are twice as many diamonds as spades and twice as many hearts as diamonds. How many clubs does he hold ?
The taxi charges in a city comprise of a fixed charge, together with the charge of the distance covered. For a journey of 16 km, the charges paid are Rs. 156 and for a journey of 24 km, the charges paid are Rs. 204. What will a person have to pay for travelling a distance of 30 km?
If every 2 out of 3 readymade shirts need alterations in the sleeves, and every 4 out of 5 need it in the body, how many alterations will be required for 60 shirts ?
At the end of a business conference the ten people present all shake hands with each other once. How many handshakes will there be altogether ?
After distributing the sweets equally among 25 children, 8 sweets remain. Had the number of children been 28, 22 sweets would have been left after equal distribution. What was the total number of sweets ?
A group of 1200 persons consisting of captains and soldiers is travelling in a train. For every 15 soldiers there is one captain. The number of captains in the group is
In a caravan, in addition to 50 hens, there are 45 goats and 8 camels with some keepers. If the total number of feet be 224 more than the number of heads in the caravan, the number of keepers is
A monkey climbs 30 feet at the beginning of each hour and rests for a while when he slips back 20 feet before he again starts climbing in the beginning of the next hour. If he begins his ascent at 8.00 a.m., at what time will he first touch a flag at 120 feet from the ground?
A number consists of two digits whose sum is 11. If 27 is added to the number, then the digits change their places. What is the number ?
An enterprising businessman earns an income of Re. 1 on the first day of his business. On every subsequent day, he earns an income which is just double of that made on the previous day. One the 10th day of business, his income is
|
88 videos|119 docs|91 tests
|
|
88 videos|119 docs|91 tests
|


 3x = 48
3x = 48  x = 16.
x = 16.

 4x + 2y = 2x + 2y + 14
4x + 2y = 2x + 2y + 14  2x = 14
2x = 14  x = 7.
x = 7.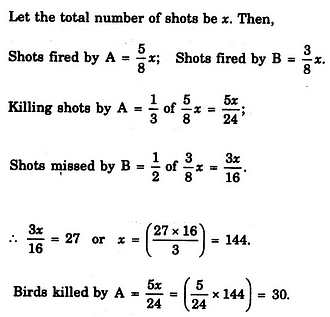

 2x + 14 = 3x - 9
2x + 14 = 3x - 9  x = 23.
x = 23.
 14x = 112
14x = 112  x = 8.
x = 8.
 20x + 25 (324 - x) = 7100
20x + 25 (324 - x) = 7100 5x= 1000
5x= 1000  x = 200. Hence, number of 25-paise coins = (324 - x) - 124.
x = 200. Hence, number of 25-paise coins = (324 - x) - 124. 6x = 6
6x = 6  x - 1.
x - 1.
 (25x - 14) is divisible by 28
(25x - 14) is divisible by 28  28x - (3x + 14) is divisible by 28
28x - (3x + 14) is divisible by 28 (3x + 14) is divisible by 28
(3x + 14) is divisible by 28  x = 14.
x = 14. 9x + 38 = 110 - 9x
9x + 38 = 110 - 9x  18x = 72
18x = 72  x = 4.
x = 4.














