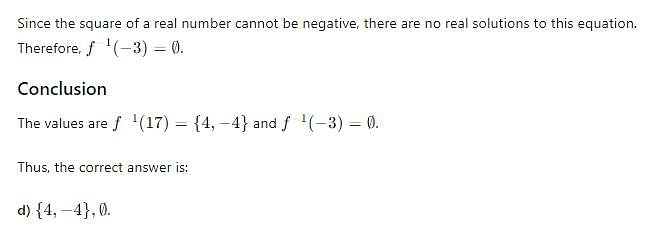All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Quantitative Aptitude (Quant)  >  Test: Set Theory- 2 - CAT MCQ

Test: Set Theory- 2 - CAT MCQ


Test Description

10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Set Theory- 2

Test: Set Theory- 2 for CAT 2025 is part of Quantitative Aptitude (Quant) preparation. The Test: Set Theory- 2 questions and answers have been prepared according to the CAT exam syllabus.The Test: Set Theory- 2 MCQs are made for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Set Theory- 2 below.
Solutions of Test: Set Theory- 2 questions in English are available as part of our Quantitative Aptitude (Quant) for CAT & Test: Set Theory- 2 solutions in Hindi for Quantitative Aptitude (Quant) course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: Set Theory- 2 | 10 questions in 10 minutes | Mock test for CAT preparation | Free important questions MCQ to study Quantitative Aptitude (Quant) for CAT Exam | Download free PDF with solutions
Test: Set Theory- 2 - Question 1
Save

The number of elements in the power set of the set {{a, b}, c} is

Detailed Solution for Test: Set Theory- 2 - Question 1

We can simply solve this problem by using the following mathematical process.

A power set is defined as the set or group of all subsets for any given set, including the empty set.  A set that has 'n' elements has 2n subsets in all.

The power set is denoted by the notation P(S) and the number of elements of the power set is given by 2n.

In the given set, the number of elements is 2

Therefore, in the power set, the number of elements will be

Hence, The number of elements in the power set of the set {{a,b},c} is 4.

Test: Set Theory- 2 - Question 2
Save

 If R = ((1, 1), (3, 1), (2, 3), (4, 2)), then which of the following represents R2, where R2 is R composite R?

Detailed Solution for Test: Set Theory- 2 - Question 2

The correct answer is D as
 R = ((1, 1), (3, 1), (2, 3), (4, 2))
RoR=R2=((1, 1), (3, 1), (2, 3), (4, 2))((1, 1), (3, 1), (2, 3), (4, 2))
     =((1, 1), (3, 1), (2, 1), (4, 3))
take the first set (1,1) then take the second element of this subset check in the other set R is there any starting with 1 if yes then take its second element and make a subset in R2 similarly check for all.
like (4,2) (2,3)=(4,3)in R2

Clear all your doubts with EduRev
Test: Set Theory- 2 - Question 3
Save

In a room containing 28 people, there are 18 people who speak English, 15 people who speak Hindi and 22 people who speak Kannada, 9 persons speak both English and Hindi, 11 persons speak both Hindi and Kannada where as 13 persosn speak both Kannada and English. How many people speak all the three languages ?

Detailed Solution for Test: Set Theory- 2 - Question 3

Let X was the people who speaks all three languages.
Total number of people = (Hindi + English + Kannad) - (Hindi and English + Hindi and Kannad + Kannad and English) + X

28 = (15 + 22 + 18) - (9 + 11 + 13) +X

X = 28 - 55 + 33

X = 6.

Test: Set Theory- 2 - Question 4
Save

Order of the power set of a set of order n is
Test: Set Theory- 2 - Question 5
Save

If f : R ---->R defined by f(x) = x2 + 1, then values of f -1 (17) and  f -1(-3) are respectively
Detailed Solution for Test: Set Theory- 2 - Question 5



Test: Set Theory- 2 - Question 6
Save

In a beauty contest, half the number of experts voted for Mr. A and two thirds voted for Mr. B. 10 voted for both and 6 did not vote for either. How many experts were there in all ?
Detailed Solution for Test: Set Theory- 2 - Question 6

The correct answer is C as
Let,the number of voters (experts) be denoted as x
A/Q
 X/2+2x/3-10+6=x
7x/6-4=x
7x-24=6x
x=24
 

Test: Set Theory- 2 - Question 7
Save

Let n(A) denotes the number of elements in set A. If n(A) =p and n(B) = q, then how many ordered pairs (a, b) are there with a ∈ A and b ∈ B ?
Test: Set Theory- 2 - Question 8
Save

The set of all Equivalence classes of a set A of cardinality C
Test: Set Theory- 2 - Question 9
Save

Let Z denote the set of all integers.
Define f : Z —> Z by
f(x) = {x / 2 (x is even)
            0     (x is odd)
then f is
Test: Set Theory- 2 - Question 10
Save

Let R be a relation "(x -y) is divisible by m", where x, y, m are integers and m > 1, then R is
Detailed Solution for Test: Set Theory- 2 - Question 10

a) Since x - x = 0, m
=> x - x is divisible by m
(x,x) ∈ R
=> R is reflexive
b) Let (x,y) ∈ R
=> x - y = mq for some q ∈ I
=> y - x = m(-q)
y - x is divisible by m
(y,x) ∈ R
=> R is symmetric.
c) Let (x,y) and (y,z) ∈ R
=> x - y is divisible by m and y - z is divisible by m
=> x - y = mq and y - z = mq' for some q, q' ∈ I
=>(x-y)+(y-z) = m(q+q')
=> x - z = m(q + q'), q + q' ∈ I
(x,z) ∈ R
=> R is transitive.
Hence the relation is equivalence relation.

191 videos|133 docs|110 tests
Join Course
Information about Test: Set Theory- 2 Page
In this test you can find the Exam questions for Test: Set Theory- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Set Theory- 2, EduRev gives you an ample number of Online tests for practice
191 videos|133 docs|110 tests
Join Course
Download as PDF

Important Questions for Set Theory- 2

Find all the important questions for Set Theory- 2 at EduRev.Get fully prepared for Set Theory- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Set Theory- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Set Theory- 2 resources.

Set Theory- 2 MCQs with Answers

Prepare for the Set Theory- 2 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Set Theory- 2 Quantitative Aptitude (Quant)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Set Theory- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup