Test: Venn Diagrams- 2 - CAT MCQ
10 Questions MCQ Test - Test: Venn Diagrams- 2
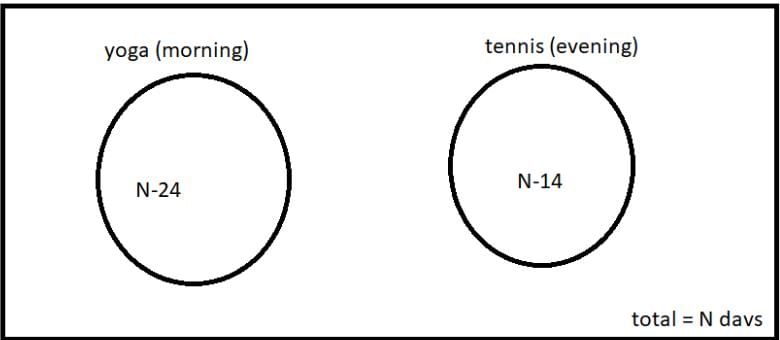
Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
How many schools had none of the three viz., laboratory, library or play – ground?
What was the ratio of schools having laboratory those having library?
A survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.
What is the maximum percentage of people who can watch all the three channels?
A survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.
If 5% of people watched DD and CNN, 10% watched DD and BBC, then what percentage of people watched BBC and CNN only?
A survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.
Referring to the previous question, what percentage of people watched all the three channels?
Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
If A = {62n - 35n-1}, where n = 1,2,3, ... and B = {35(n-1)}, where n = 1,2,3, ... then which of the following is true?