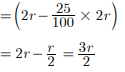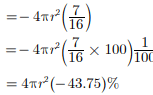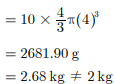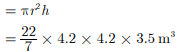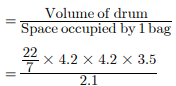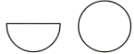Test: Surface Area & Volumes- Assertion & Reason Type Questions - Class 9 MCQ
10 Questions MCQ Test Class 9: Additional Practice - Test: Surface Area & Volumes- Assertion & Reason Type Questions
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : If diameter of a sphere is decreased by 25%, then its curved surface area is decreased by 43.75%.
Reason : Curved surface area is increased when diameter decreases
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : The external dimensions of a wooden box are 18 cm, 10 cm and 6 cm respectively and thickness of the wood is 15 mm, then the internal volume is 765 cm3.
Reason : If external dimensions of a rectangular box be l, b and h and the thickness of its sides be x , then its internal volume is (l - 2x) (b - 2x) (h - 2x).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
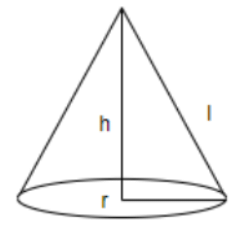
Assertion : The total surface area of a cone whose radius is r/2 and slant height 2l is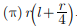 
Reason : Total surface area of cone is (π)r(l+r) where r is radius and l is the slant height of the cone.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : A cone is a solid figure.
Reason : A cone is generated when rectangular sheet is rotated about its axis
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : In a cylinder, if radius is halved and height is doubled, the volume will be halved.
Reason : In a cylinder, radius is doubled and height is halved, curved surface area will be same.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : If the inner dimensions of a cuboidal box are 50 cm x 40 cm x 30 cm , then the length of the longest rod that can be placed in the box is 50√2 cm.
Reason : The line joining opposite corners of a cuboid is called its diagonal.
Also, length of longest rod = length of diagonal.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : A shot put is a metallic sphere of radius 4 cm. If the density of the metal is 10 g per cm3. then the mass of the shot put is 2 kg.
Reason : Volume of sphere of radius r is 4/3 πr3.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : An edge of a cube measures r cm. If the largest possible right circular cone is cut out of this cube, then the volume of the cone is 1/3 πr3.
Reason : Volume of the cone is given by 1/3 πr2h, where r is the radius of the base and h is the height of the cone.
Direction: In the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
Assertion : Into a circular drum of radius 4.2 m and height 3.5 m, the number of full bags of wheat can be emptied, if the space required for wheat in each bag is 2.1 cu. m, is 92 bags nearly.
Reason : Volume of circular drum is 1/3 πr2h where r is radius and h is height of drum.
Direction: In the section, this question has two matching lists. Choices for the correct combination of elements from Column-I and Column-II are given as options (a), (b), (c) and
(d) out of which one is correct.
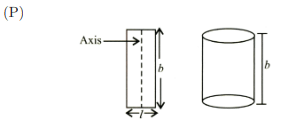
Q. Match the description given in Column-I with their corresponding solid figure in Column-II.
|
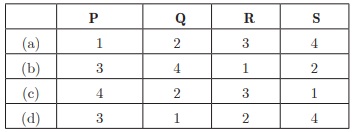
4 docs|108 tests
|
Important Questions for Surface Area & Volumes- Assertion & Reason Type Questions
Surface Area & Volumes- Assertion & Reason Type Questions MCQs with Answers
Online Tests for Surface Area & Volumes- Assertion & Reason Type Questions Class 9: Additional Practice
|
© EduRev
|
Education Revolution
|
|
