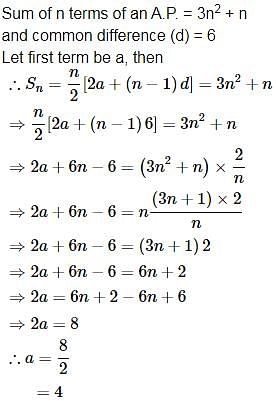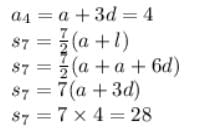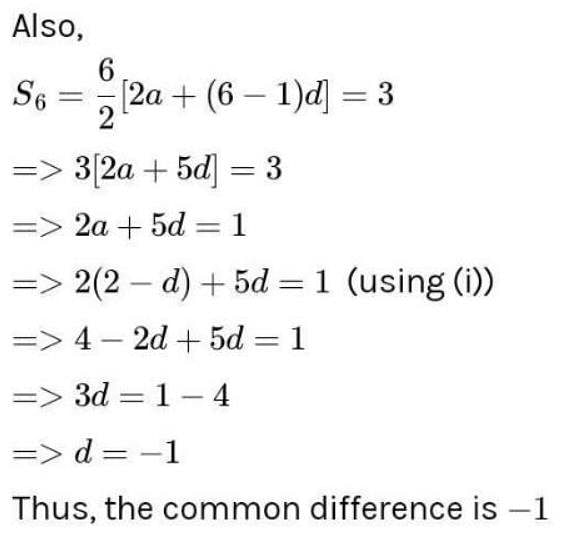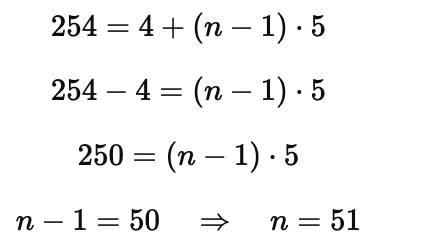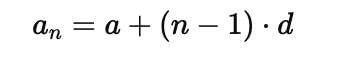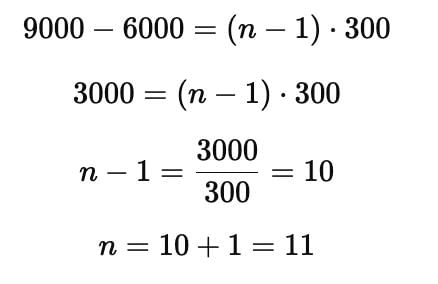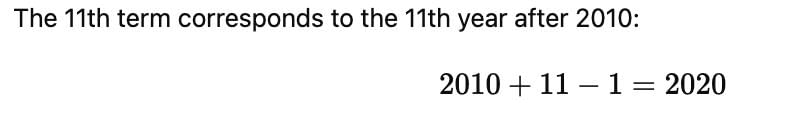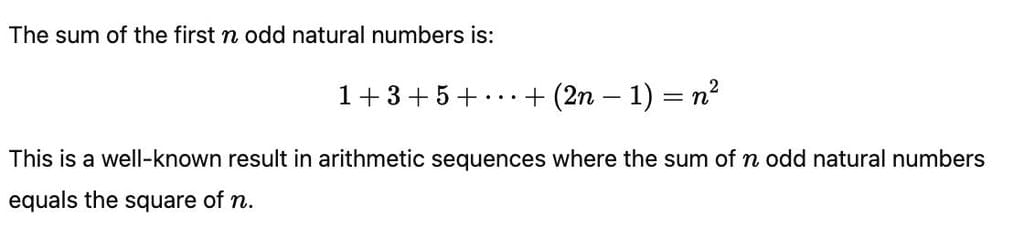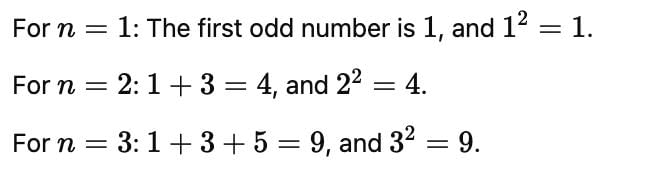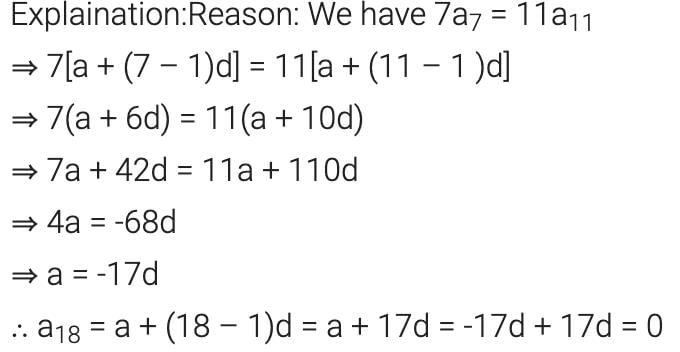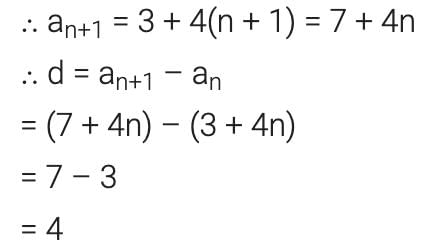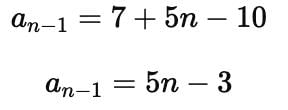Practice Test: Arithmetic Progressions - Class 10 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 10 - Practice Test: Arithmetic Progressions
If the sum of first n terms of an AP be 3n2 + n and it's common difference is 6, then its first term is :
If 7th and 13th terms of an A.P. be 34 and 64, respectively, then it's 18th term is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The sum of all 2-digit odd positive numbers is :
The fourth term of an A.P. is 4. Then the sum of the first 7 terms is :
In an A.P. s3 = 6, s6 = 3, then it's common difference is equal to :
The 15th term from the last term of the AP: 4,9,14,......254 is :
Ramesh started work in 2010 with an annual salary of ₹6000 and received an increment of ₹300 each year. In which year did his income reach ₹9000?
If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then 18th term is
Find the sum of 12 terms of an A.P. whose nth term is given by an = 3n + 4
The nth term of an A.P. is given by an = 3 + 4n. The common difference is
The (n – 1)th term of an A.P. is given by 7,12,17, 22,… is
If {an} = {2.5, 2.51, 2.52,...} and {bn} = {3.72, 3.73, 3.74,...} be two AP's, then a100005 – b100005 =
In an Arithmetic Progression, if a = 28, d = -4, n = 7, then an is:
The sum of the first four terms of an A.P. is 56. The sum of the last four terms is 112. If its first term is 11, then find the number of terms.
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|