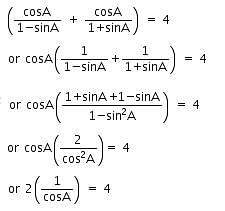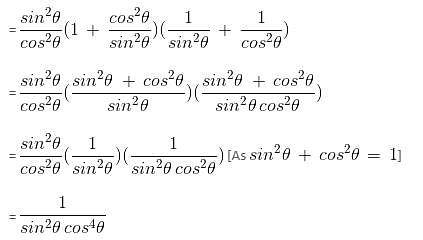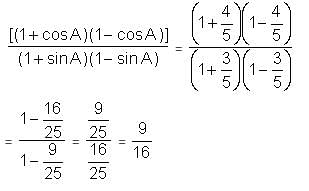Test Level 1: Trigonometry - 2 - CAT MCQ
15 Questions MCQ Test Level-wise Tests for CAT - Test Level 1: Trigonometry - 2
From a 60 m high building, the angles of depression of two cars on the opposite ends of the building are observed to be 60° and 30°. Find the distance between the cars, if the line joining them passes through the foot of the building.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A right triangle PQR is right-angled at Q. If tan R = 1/√3, then which of the following is the value of sin R?
If sin 30° = 1/2 , the value of expression tan 30° - sin 15° cos 15° is
In a right triangle ABC, right-angled at B, cot2 A = 9/16. What is the value of cos A?
Find the value of sec 30° cot 30° tan 30° cosec 30°.
If m = 1 + tan2θ and n = 1 + cot2θ, then m/n equals
If sinθ = 3/5, then find the value of (cosθ + tanθ + cotθ).
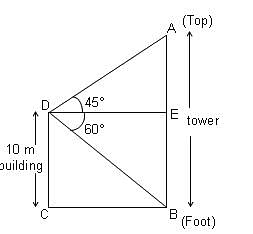
From the top of a 10 m high building, the angle of elevation of the top of a tower is 45° and the angle of depression of its foot is 60°. How will you represent this situation diagrammatically?
The reduced form of cos6 x + sin6 x + 3 cos2 x.sin2 x is _______________.
If in a right triangle, tan A = 3/4 , then find the value of
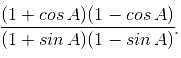
From two points A and B on the opposite sides of a tower, the angles of elevation to the top of the tower are 45° and 30°, respectively. If the height of the tower is 120 m, then find the distance between A and B, corrected to two decimal places.
|
5 docs|272 tests
|




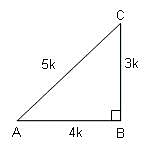




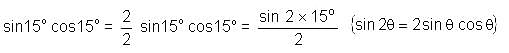
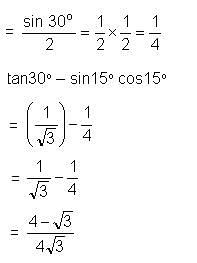
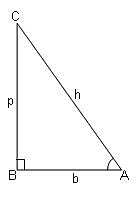

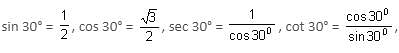
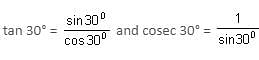
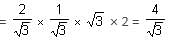
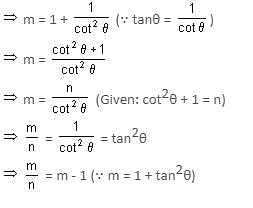

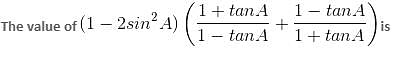
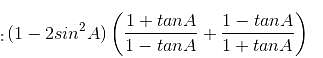
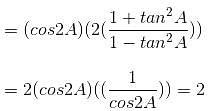
 then what is the value of A?
then what is the value of A?