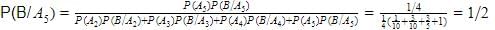Test: Bayes’ Theorem - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Bayes’ Theorem
An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is:
A bag ‘A’ contains 2 white and 3 red balls and a bag ‘B’ contains 4 white and 5 red balls. One ball is drawn at random from one of the bags and is found to be red. The probability that it was drawn from bag B is:
If A and B are two events such that and P(B) ≠ 0, then which of the following is correct?
A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, and scooter or by other means of transport are respectively 0.3, 0.2, 0.1 and 0.4. The probabilities that he will be late are 1/4 , 1/3 and 1/12, if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. The probability that he comes by bus is:
The conditional probability P(Ei |A) is called a ……… probability of the hypothesis Ei.
Let {E1, E2, …, En} be a partition of the sample space S, and suppose that each of the events E1, E2,…, En has nonzero probability of occurrence. Let A be any event associated with S, then
Probability that A speaks truth is 5/9 . A coin is tossed and reports that a head appears. The probability that actually there was head is:
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
|
204 videos|290 docs|139 tests
|