IPMAT Mock Test - 1 (New Pattern) - Commerce MCQ
30 Questions MCQ Test IPMAT Mock Test Series - IPMAT Mock Test - 1 (New Pattern)
The number obtained on rationalizing the denominator of 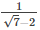 is
is
A shopkeeper sells 200 shirts and makes a profit equal to the selling price of 25 shirts. Find his profit percentage.
If m : n = 3 : 2, then (4m + 5n) : (4m − 5n) is equal to = ?
Direction: Study the given bar graph carefully and answer the questions given below.
The following bar graph shows the number of Male and Female customers who visited a restaurant for 6 days of a week.
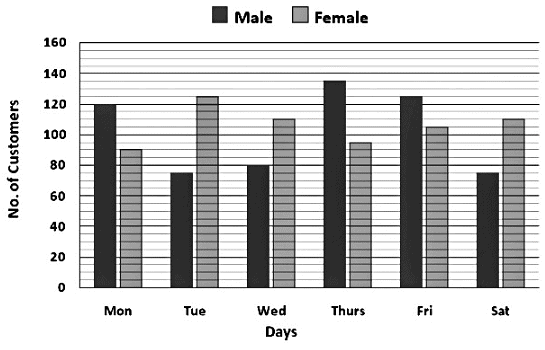
Q. What is the difference between the average number of Males and Females visiting the restaurant?
Direction: Study the given bar graph carefully and answer the questions given below.
The following bar graph shows the number of Male and Female customers who visited a restaurant for 6 days of a week.
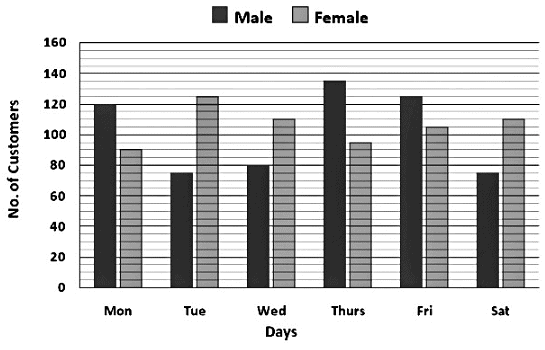
Q. What is the ratio between the number of Males visiting the restaurant on Tuesday, Thursday and Friday together and the number of females visiting the restaurant on the same days?
Direction: Study the given bar graph carefully and answer the questions given below.
The following bar graph shows the number of Male and Female customers who visited a restaurant for 6 days of a week.
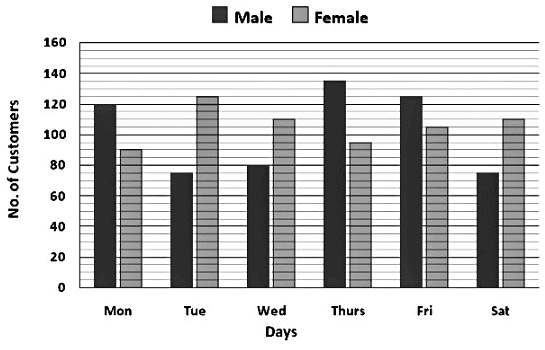
Q. Out of the total number of customers visiting the restaurant on Monday, Wednesday and Friday 40% have pre-booking of tables in the restaurant and the total number of customers visiting the restaurant on the remaining days 60% have pre-booked their tables. What is the sum of the customers who have pre-booking in the restaurant?
Direction: Study the given bar graph carefully and answer the questions given below.
The following bar graph shows the number of Male and Female customers who visited a restaurant for 6 days of a week.
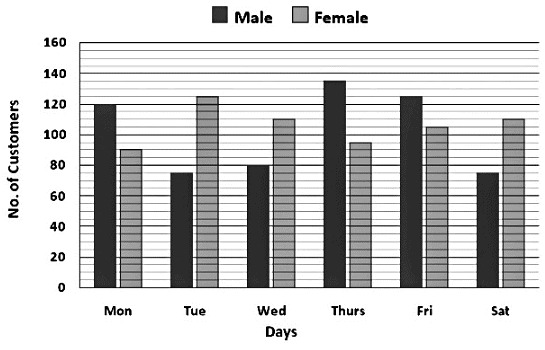
Q. The number of customers visiting the restaurant on Sunday is 30% more than the number of customers visiting the restaurant on Wednesday and the ratio of male and female is 8 ∶ 5, then the number of males visiting the restaurant on Sunday is what percent of Males visiting the restaurant on Monday?
The value of x − yx−y when x = 2 and y = −2 is:
The product of two numbers is 120 and the sum of their squares is 289. The sum of the two number is:
The average of some natural numbers is 15. If 30 is added to the first number and 5 is subtracted from the last number the average becomes 17.5 then the number of natural numbers is:
Find the nth term of the following sequence:
5 + 55 + 555 +….Tn
Two trains running in opposite directions cross a man standing on the platform in 27 seconds and 17 seconds respectively and they cross each other in 23 seconds. The ratio of their speeds is:
Which one of the following is an example of the empty set?
The first term of an Arithmetic Progression is 22 and the last term is −11. If the sum is 66, the number of terms in the sequence are:
What is the value of 1/2 log1025 –2log103 + log1018?
A sum of money becomes 5 times at simple interest in 16 years. What is the rate of interest?
If x2 − 2pxy − y2 = 0 and x2 − 2qxy − y2 = 0 bisect angles between each other, then:
If A = {1, 4}, B = {2, 3}, C = {3, 5} then (A × B) ∩ (A × C) is equal to:
The relation R on the set of integer is given by R = {(a, b) : a − b is divisible by 7, where a, b ∈ Z}, then R is a/an:
The distance between two points A and B is 600 km. When they start moving towards each other they meet in 12 hours. If A started moving 5 hours after B, then they meet in 10 hours. Taking these into account find the speed of B.
car covers a distance of 4 km in 6 minutes. If it's speed is decreased by 2 km/hr, then find the time taken by the car to cover same distance.
|
9 videos|39 docs|10 tests
|


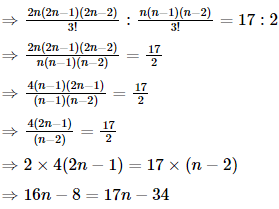
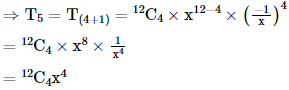

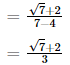
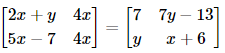
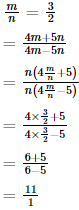

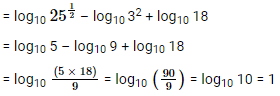
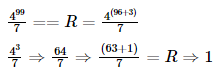
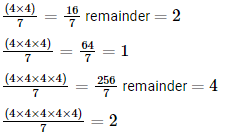
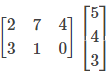 is
is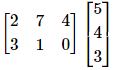 is possible.
is possible.















