IPMAT Mock Test - 2 (New Pattern) - Commerce MCQ
30 Questions MCQ Test - IPMAT Mock Test - 2 (New Pattern)
In an examination, a candidate has to pass in each of the 5 subjects. In how many ways he can fail?
A certain sum is given on Compound Interest at some rate. The sum amounts to Rs. 7350 and Rs. 8575 at the end of 2 years and 3 years respectively. The sum given on Compound Interest is:
A two-digit number is such that the product of its digits 12. When 36 is added to this number, the digits interchange their places, The number is:
The average of seven consecutive odd numbers (in increasing order) is k. If the next four consecutive odd numbers are included, then the average of all the number is:
A man leaves from P at 6 AM and reaches Q at 2 PM on the same day. Another man leaves Q at 8 AM and reaches P at 3 PM on the same day. At what time do they meet?
'A' invests Rs. 10000 for 3 years at a certain rate of interest. At the end of the second year, it amounts to Rs. 11664. Calculate the rate of interest per annum, if interest is compounded annually:
The equation of the tangents to the ellipse 4x2 + 5y2 = 20 which are perpendicular to line 3x + 2y - 5 = 0 is:
What is the sum of the squares of direction cosines of the line joining the points (1, 2, −3) and (−2, 3, 1)?
A card is drawn from a pack of 52 cards. The probability of getting a queen of club or a king of heart is:
A and B are two stations 1200 km apart train X starts from station A towards station B at 60 kmph 2 hours before train Y starts from station B towards station A. If they meet at a point 360 km from station B. What is the speed of train Y?
If A + B + C = π , then sin (A + B) + sin C is equal to:
Suresh loses 15% when he sells his computer for Rs. 17000. If he sells it for Rs. 20448, then his loss/profit percentage is:
Direction: The bar graph given below shows the Sale (in thousands) of six branches of a company during two consecutive years 2016 and 2017.
Sale (in thousand numbers) of Six Branches - A, B, C, D, E and F of a Company in 2016 and 2017.
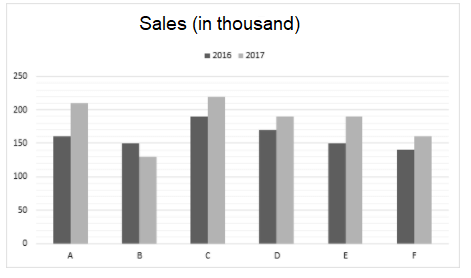
Total Sale of branches A, C and E together for both the years (in thousands) is:
The bar graph given below shows the Sale (in thousands) of six branches of a company during two consecutive years 2016 and 2017.
Sale (in thousand numbers) of Six Branches - A, B, C, D, E and F of a Company in 2016 and 2017.
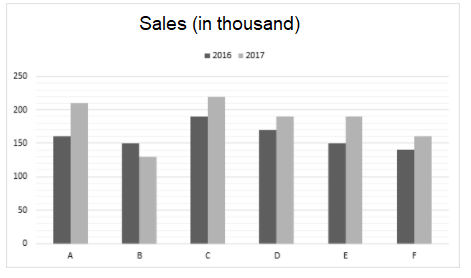
What is the ratio of the total Sale of branch D for both the years to the total Sale of branch B for both the years?
If x + 2y ≤ 3, x > 0 and y > 0, then one of the solution is:
If A = {1, 2, 3, 4, 6} and R is a relation on A such that R = {(a, b) : a, b ∈ A and b is exactly divisible by a}, then find the number of elements present in range of R.
If A and B are the domain and range respectively for the relation R such that R={(1,3), (2,4),(3,5),(5,7)}, then which of the following option is true?
If A = {1, 2, 3, …, 14} and R is a relation defined on A such that R = {(x, y) : 3x − y = 0 where x, y ∈ A}, then find the range of R.
Rina bought 24 kg sugar for Rs.1056. She sold it at a profit equal to the selling price of 4 kg of it. The selling price of sugar, per kg, was:
The system of equations:
2x + y - 3z = 5
3x - 2y + 2z = 5 and
5x - 3y - z = 16
The union of the two sets A = {1, 2, 7, 9, 12} and B = {x : x2 − 10x + 16 = 0} is:
Let ![]() denote the complements of two sets P and Q. Then the set (P − Q) ∪ (Q − P) ∪ (P ∩ Q) is:
denote the complements of two sets P and Q. Then the set (P − Q) ∪ (Q − P) ∪ (P ∩ Q) is:
If 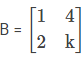 is a singular matrix, then value of k = _______.
is a singular matrix, then value of k = _______.
The 480 m long train can cross the same length of the train with the same speed in opposite direction in 8 seconds. What is the speed of the train?
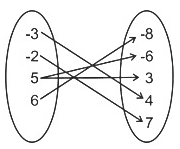
In the ordered set of pairs {(−3, 4), (5, −6), (−2, 7), (5, 3), (6, −8)} the domain and range will form:
Find the smallest value of (a − b) so that 42a48b(a > b) is divisible by 11.



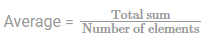

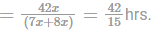
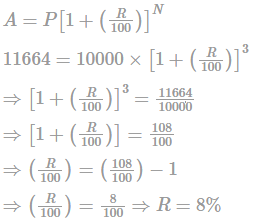
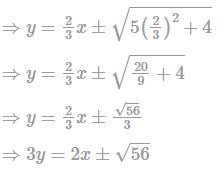
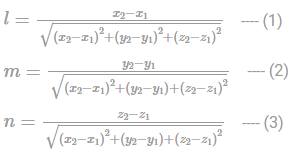

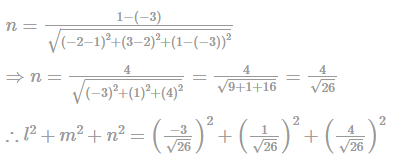
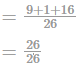
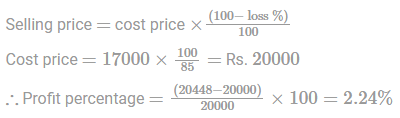
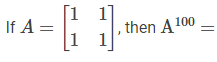
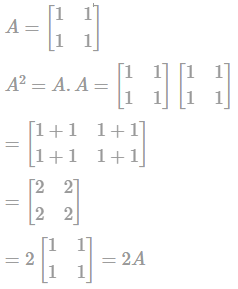
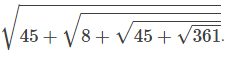
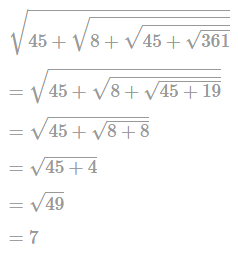
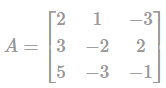
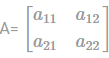 is a square matrix of order 2 then the determinant is given by:
is a square matrix of order 2 then the determinant is given by: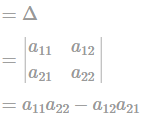
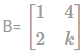 is a singular matrix
is a singular matrix