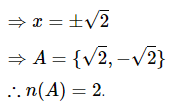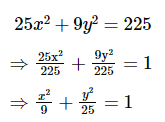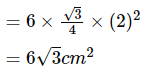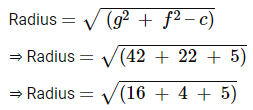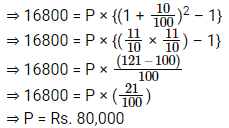IPMAT Mock Test - 10 (New Pattern) - Commerce MCQ
30 Questions MCQ Test IPMAT Mock Test Series - IPMAT Mock Test - 10 (New Pattern)
If 0 < x < 2π, then which of the following is the solution of the equation cot x + 1 + √2 = 0?
If A = {x ∈ R : x2 = 2} and B = {y ∈ R : y2 − 5y + 6 = 0}. Find n(A × B).
A train started from station A and preceded towards station B at a speed of 80 km/hr 45 minutes later, another train started from station B towards A at the speed of 90 km/hr. If the distance between station A and Station B is 400 km. Find the distance at which both trains meet from A-
Find the length of the latus rectum of the ellipse 25x2 + 9y2 = 225
Consider the proper subsets of {1, 2, 3, 4}. How many of these subsets are a superset of the set {3}?
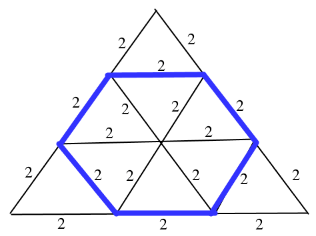
An equilateral triangle of side 6cm has its corners cut off to form a regular hexagon. Area (in cm2 ) of this regular hexagon will be?
76n − 66n, where n is an integer > 0, is divisible by
Find the radius of circle x2 + y2 – 8x – 4y – 5 = 0
In a certain store, the profit is 320% of the cost. If the cost increases by 25% but the selling price remains constant, approximately what percentage of the selling price is the profit?
Direction: Study the data carefully and answer the questions given below:
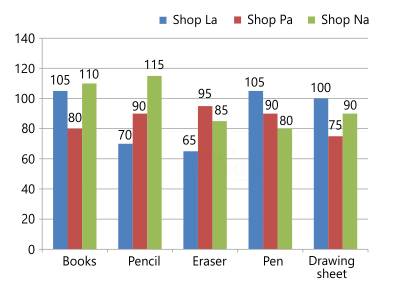
If the total profit earned by all the shop by selling the eraser is Rs 735, find the total profit earned by Shop La and Shop Pa after selling the eraser. (If the cost price and selling price are equal for all the erasers.)
Direction: Study the data carefully and answer the questions given below:
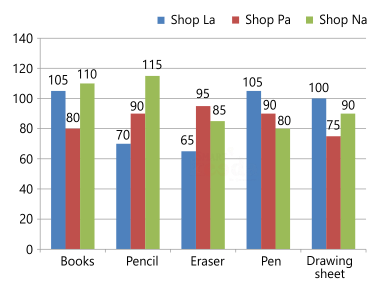
The cost price of the drawing sheet sold by Shop Pa is Rs 12. If shopkeeper wants to earn 25% profit after giving 25% discount. Find the total discount given by Shop Pa after selling 4/5 of the drawing sheet.
Direction: Study the data carefully and answer the questions given below:
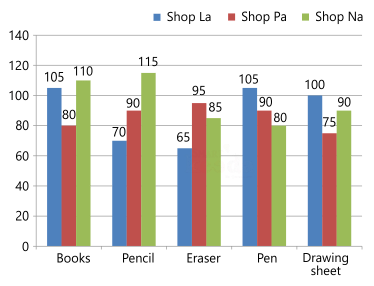
What is the ratio of the number of books sold by shop La and Na together to the number of pens sold by shop Pa and Na?
If A : {x : x = 4n, n ∈ Z} and B = {x : x = 6n, n ∈ Z}, then
The compound interest on a sum of money for 2 years at 10% per annum is Rs. 16800. Find the simple interest for 3 years at the same rate of interest and the same sum.
If the length of a certain rectangle is decreased by 4 cm and the width is increased by 3 cm, a square with the same area as the original rectangle would result. Find the perimeter of the original rectangle.
If A = {1, 2, 3, 4, 5, 6} and R is a relation on A such that R = {(x, y) : y = x + 1, where x and y ∈ R}, then find the domain of R?
If log (x + 2) + log (x − 2) = log 5 then the value of x will be
Karishma bought two necklace for Rs. 1,39,500.00. She sold one of them for Rs. 75,000.00 and the other one for Rs. 80,000.00. How much money did she gain?
Set of values of m for which two points P and Q lie on the line y = mx + 8 so that ∠APB = ∠AQB = π/2 where A ≡ (−4, 0), B ≡ (4,0) is:
What is the least number of soldiers that can be drawn up in troops of 12, 15, 18 and 20 soldiers and also in form of a solid square?
In how many ways can 4 girls and 5 boys be arranged in a row so that all the four girls are together?
If A and B are the domain and range respectively for the relation R such that R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}} then which of the following option is true?
The percentage profit earned by selling an article for Rs. 1920 is equal to the percentage loss incurred by selling the same article for Rs. 1280. At what price should the article be sold to make 25% profit?
|
9 videos|39 docs|10 tests
|


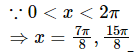

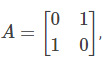 then the matrix A is a/an:
then the matrix A is a/an: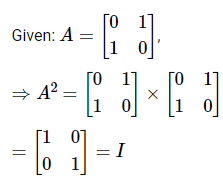
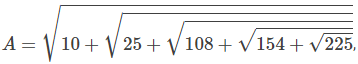 find the value of AA.
find the value of AA.