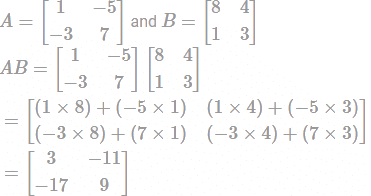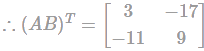IPMAT Mock Test - 9 (New Pattern) - Commerce MCQ
30 Questions MCQ Test IPMAT Mock Test Series - IPMAT Mock Test - 9 (New Pattern)
If A = 315∘ then find the value of 3(tan2 A + cotA − 3)2?
Direction: Study the following graph carefully and answer the question that follows.
The number of students from four different schools who qualified in an exam in six different years from 2012 to 2017 is shown in the graph given below.
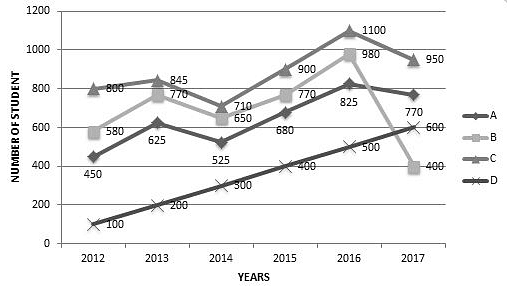
What was the total number of students who qualified in the exam from school A in 2016, from school B in 2015, from school C in 2014 and from school D in 2012?
Direction: Study the following graph carefully and answer the question that follows.
The number of students from four different schools who qualified in an exam in six different years from 2012 to 2017 is shown in the graph given below.
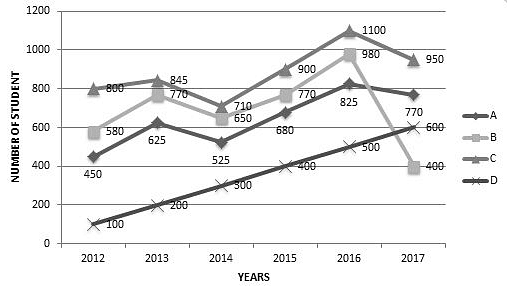
What was the average number of students who qualified in the exam from school C over all the years together?
Direction: Study the following graph carefully and answer the question that follows.
The number of students from four different schools who qualified in an exam in six different years from 2012 to 2017 is shown in the graph given below.
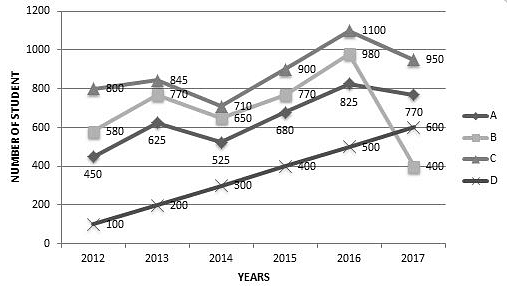
What was the difference between the total number of students who qualified in the exam from schools A and B together in the year 2017 and the total number of students who qualified in the exam from schools C and D together in the year 2015?
If X={4n − 3n − 1, n ∈ N} and Y = {9n − 9, n ∈ N}, then X ∪ Y is equal to:
If the sum of n numbers in the GP 4, 8, 16,… is 2044 then n is?
In a factory, the average salary of the employees is Rs. 1500. After the inclusion of 5 employees, the total salary increased by Rs. 3000 and the average salary was reduced by Rs. 100, then now the number of employees are:
The average age of 3 sisters is 15. If the ages of 2 sisters are 12 years and 15 years, the age of the third sister is:
On selling an article for Rs. 265 a man loses 4%. In order to gain 12%, for how much he must sell the article?
The divisor is 25 times the quotient and 5 times the remainder. If the quotient is 16, the dividend is:
In a two digit number, the digit at the unit's place is 1 less than twice the digit at the ten's place. If the digits at unit's and ten's place are interchanged, the difference between the new and the original number is less than the original number by 20. The original number is:
If 432P1 is completely divisible by 9, then what is the value of P?
A man completes a certain journey by a car. If he covered 30% of the distance at the speed of 20kmph, 60% of the distance at 40km/h and the remaining of the distance at 10 kmph, his average speed is:
Shikha invested a total of Rs. 1500 in two different schemes offering simple interest of 6% and 4% respectively. In two years' time, the scheme offering higher interest rate gives Rs. 100 more interest than the scheme offering the lower rate. What was the ratio of amount invested at higher interest rate to the other amount?
In how many ways can a team of 6 members be selected from 7 boys and 4 girls, consisting of equal number of boys and girls.
If x, y, z are three consecutive positive integers, then log (1 + xz) is
Equation of the circle having diameter 8 and diameters y + 2x - 5 = 0 and 2y + 3x - 8 = 0 is?
A man completes a journey in 10 hours. He travels the first half of the journey at the rate of 21 km/hr and the second half at the rate of 24 km/hr. Find the total journey in km.
When a number n is divided by 5, the remainder is 2. When n2 is divided by 5, the remainder will be:
Direction: Study the following graph carefully and answer the question that follows.
The number of students from four different schools who qualified in an exam in six different years from 2012 to 2017 is shown in the graph given below.
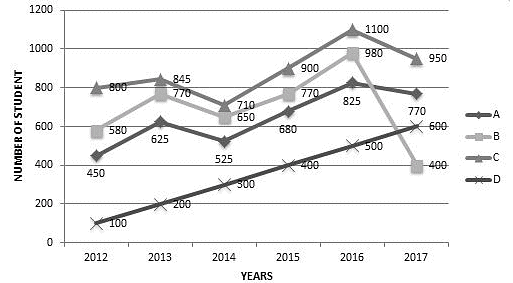
What was the ratio of the number of students who qualified in the exam from school C in the year 2014 to the number of students who qualified in the exam from school D in the year 2017?
Direction: Study the following graph carefully and answer the question that follows.
The number of students from four different schools who qualified in an exam in six different years from 2012 to 2017 is shown in the graph given below.
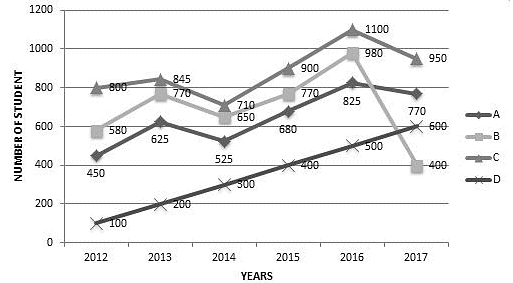
What was the approximate percentage increase in the number of students who qualified in the exam from school A in the year 2013 as compared to that in the previous year?
If A = [2, 3] then cardinality of A × A × A is:
Find the equation of the tangent to the ellipse x2 + 2y2 = 4 at the point where ordinate is 1 such that point lies in the first quadrant?
The total surface area of a cube is 108 cm2. Find the volume of the cube?
|
9 videos|39 docs|10 tests
|


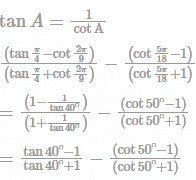
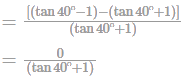

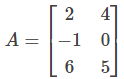
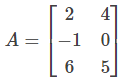
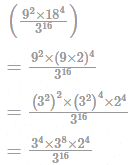
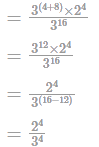
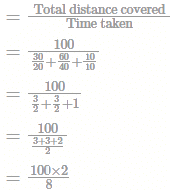
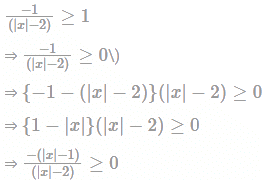
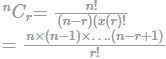
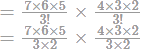
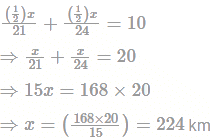
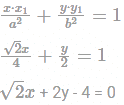
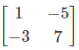 and B =
and B = 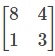 then the value of (AB)T is:
then the value of (AB)T is: