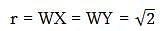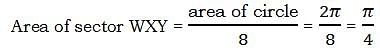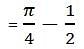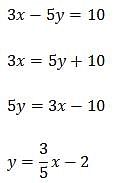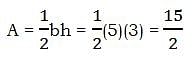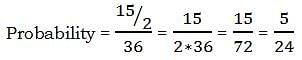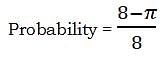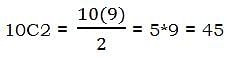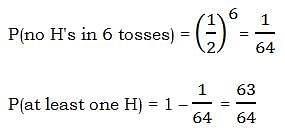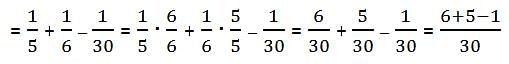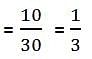Test: Probability for GMAT - 1 - GMAT MCQ
10 Questions MCQ Test Quantitative for GMAT - Test: Probability for GMAT - 1
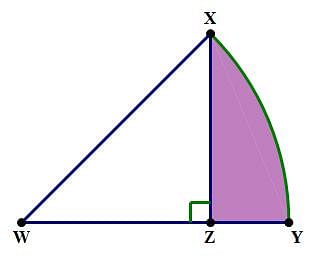
In the diagram above, WZ = XZ, and circular arc XY has a center at W. If a point is selected from anywhere within this figure, what is the probability that it is selected from the shaded region?

In the diagram above, WZ = XZ, and circular arc XY has a center at W. If a point is selected from anywhere within this figure, what is the probability that it is selected from the shaded region?
Region R is a square in the x-y plane with vertices J = (–1, –2), K = (–1, 4), L = (5, 4), and M = (5, –2). What is the probability that a randomly selected point in region R lies below the line 3x – 5y = 10?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
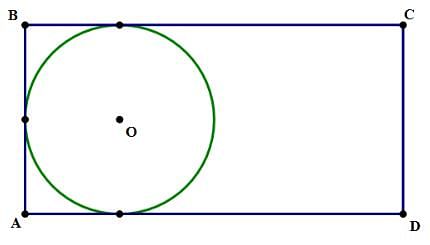
In the diagram above, the sides of rectangle ABCD have a ratio AB : BC = 1 : 2, and the circle is tangent to three sides of the rectangle. If a point is chosen at random inside the rectangle, what is the probability that it is not inside the circle?

In the diagram above, the sides of rectangle ABCD have a ratio AB : BC = 1 : 2, and the circle is tangent to three sides of the rectangle. If a point is chosen at random inside the rectangle, what is the probability that it is not inside the circle?
John has on his shelf four books of poetry, four novels, and two reference works. Suppose from these ten books, we were to pick two books at random. What is the probability that we pick one novel and one reference work?
Five children, Anaxagoras, Beatrice, Childeric, Desdemona, and Ethelred, sit randomly in five chairs in a row. What is the probability that Childeric and Ethelred sit next to each other?
In a certain game, you pick a card from a standard deck of 52 cards. If the card is a heart, you win. If the card is not a heart, the person replaces the card to the deck, reshuffles, and draws again. The person keeps repeating that process until he picks a heart, and the point is to measure: how many draws did it take before the person picked a heart and won? What is the probability that one will have at least three draws before one picks a heart?
Suppose you flip a fair coin six times. What is the probability that, in six flips, you get at least one head?
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
There are these two sets of letters, and you are going to pick exactly one letter from each set. What is the probability of picking at least one vowel?
A letter is chosen at random from the letters of the word PROBABILITY. Find the probability that letter chosen is a vowel
There are two sets of letters, and you are going to pick exactly one letter from each set.
Event A = {A, B, C, D, E}
Event B= {K, L, M, N, O, P}
What is the probability of picking a C or an M?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|