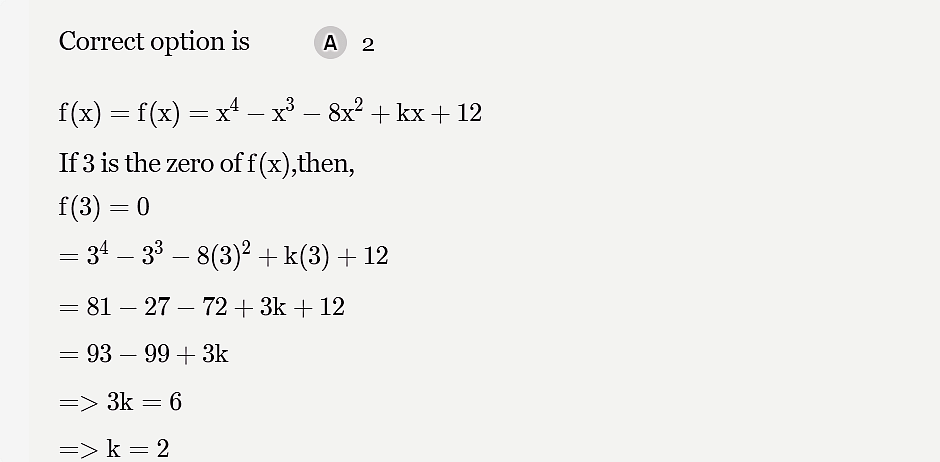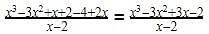Important Questions (1 Mark): Polynomials - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - Important Questions (1 Mark): Polynomials
Form a quadratic polynomial, sum of whose zeroes is 3 and product of whose zeroes is 2 solution
If x + 2 is a factor of x3 – 2ax2 + 16, then value of a is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 3 + 5 – 8 = 0, then the value of (3)3 + (5)3 – (8)3 is
If one of the factors of x2 + x – 20 is (x + 5), then other factor is
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :
If 3 is a zero of the polynomial f(x) = x4 – x3 – 8x2 + kx + 12, then the value of k is –
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –
On dividing x3 – 3x2 + x + 2 by polynomial g(x), the quotient and remainder were x – 2 and 4 – 2x respectively then g(x) :
If the polynomial 3x2 – x3 – 3x + 5 is divided by another polynomial x – 1 – x2, the remainder comes out to be 3, then quotient polynomial is –
If x + 2 is a factor of x3 – 2ax2 + 16, then value of a is
If is the zero of the cubic polynomial f(x) = 3x3 – 5x2 – 11x – 3 the other zeros are :
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most –
The graph of the quadratic polynomial ax2 + bx + c, a ≠ 0 is always –
If 2 and as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –
If α and β are the zeros of the polynomial f(x) = 16x2 + 4x – 5 then is equal to –
If α and β are the zeros of the polynomial f(x) = 15x2 – 5x + 6 then
is equal to –
If the sum of the two zeros of x3 + px2 +qx + r is zero, then pq =
Let a = 0 and p(x) be a polynomial of degree greater than 2. If p(x) leaves remainders a and – a when divided respectively by x + a and x – a, the remainder when p(x) is divided by x2 – a2 is
If one root of the polynomial x2 + px + q is square of the other root, then –
If α,β are the zeros of x2 + px + 1 and γ,δ be those of x2 + qx + 1, then the value of (α–γ) (β–γ) (α+δ) (β+δ) =
The quadratic polynomial whose zeros are twice the zeros of 2x2 – 5x + 2 = 0 is –
|
123 videos|457 docs|77 tests
|
|
123 videos|457 docs|77 tests
|