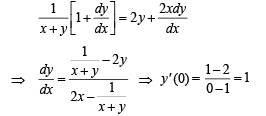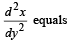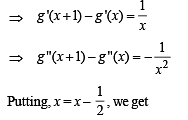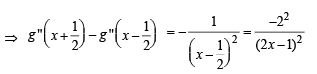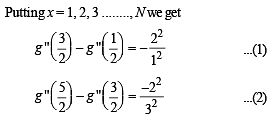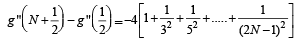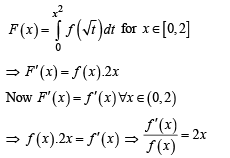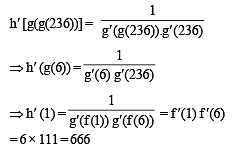JEE Advanced (Single Correct MCQs): Differentiation - JEE MCQ
11 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Differentiation
If y2 = P(x) , a polynomial of degree 3, then 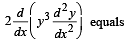
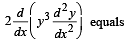
Let f (x) be a quadratic expression which is positive for all the real values of x. If g(x) = f (x) + f '(x) + f ''(x), then for any real x,
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If y is a function of x and log (x + y) – 2xy = 0, then the value of y' (0) is equal to
If f(x) is a twice differentiable function and given that f(1) = 1; f(2) = 4, f(3) = 9, then
Let g (x) = log f (x) where f (x) is twice differentible positive function on (0, ∞) such that f (x + 1) = x f (x). Then, for N = 1, 2, 3, ...........
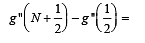
Let f : [0, 2] → R be a function which is continuous on [0, 2] and is differentiable on (0, 2) with f (0) = 1. Let
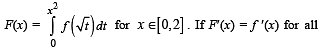
x ∈ (0,2) , then F(2) equals
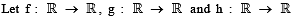 be differentiable functions such that f(x) = x3 + 3x + 2, g(f(x)) = x and h (g(g(x))) = x for all
be differentiable functions such that f(x) = x3 + 3x + 2, g(f(x)) = x and h (g(g(x))) = x for all 
|
447 docs|930 tests
|
|
447 docs|930 tests
|


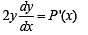 ......(2)
......(2)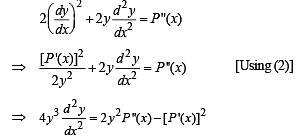
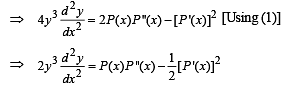
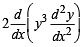
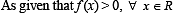
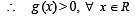
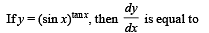

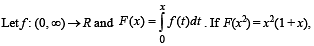 then f(4) equals
then f(4) equals