JEE Advanced Level Test: Area Under Curve With Solution - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Area Under Curve With Solution
The area bounded by [x] +[y] = 8 such that x, y > 0 is .... sq. units
Where [.] is G.I.F.
Let f : [0, ∞)→ R be a continuous and strictly increasing function such that 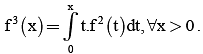 The area enclosed by y = f (x), the x-axis and the ordinate at x = 3, is
The area enclosed by y = f (x), the x-axis and the ordinate at x = 3, is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The area bounded by x = x1, y = y1 and y = -(x + 1)2 where x1, y1 are the values of x, y satisfying the equation sin-1x + sin-1y = -π will be, (nearer to origin)
Area bounded between the curves
and
be two functions and let f1(x) = max {f(t), 0 < t < x, 0 < x <} and g1(x) = min {g(t), 0 < t < x, 0 < x < 1}. Then the area bounded by f1(x) < 0, g1(x) < 0 and x-axis is
The values of the parameter a(a > 1) for which the area of the figure bounded by the pair of straight lines y2 – 3y + 2 = 0 and the curves is greatest is.
(Here [.] denotes the greatest integer function).
Area of region bounded by x2 + y2 < 4 and (|x| + |y|) < 2 is ____ square units.
The area of a circle is A1 and the area of a regular pentagon inscribed in the circle is A2 .Then A1 : A2 is
The area bounded by the curve and x-axis is
the area of the region bounded by y = x and y = x+ sin x is
The area bounded by the curves y = x2, y = [x+1], x < 1 and the y - axis, where[.] denotes the greatest integer not exceeding x, is
The area of the smaller region in which the curve denotes the greatest integer function, divides the circle (x – 2)2 + (y + 1)2 = 4, is equal to
The area bounded by the curves y = 2- |x -1| , y = sin x ; x = 0 and x =2 is
A curve passes through the point (0,1)and has the property that the slope of the curve at every point P is twice the y–coordinate of P . If the area bounded by the curve, the axes of coordinates and the line
The area bounded by the curve (y – arc sinx)2 = x – x2, is
The area of the region enclosed by the curve 5x2 + 6xy + 2y2 + 7x + 6y + 6 = 0 is
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), the xaxis and the two ordinates x = 0 and
The area enclosed between the curves y = sin4x cos3x, y = sin2xcos3x between x = 0 and
The area of the region bounded by the curves which contains (1, 0) point in its interior is
Area bounded by the curves y = ex , y= loge x and the lines x = 0, y = 0, y = 1 is
A circular arc of radius ‘1’ subtends an angle of ‘x’ radians, as shown in the figure. The point ‘R’ is the point of intersection of the two tangent lines at P & Q. Let T(x) be the area of triangle PQR and S(x) be area of the shaded region. Then
A point P moves inside a triangle formed by such that min {PA, PB, PC} = 1. The area formed by the curve traced by P is ....... sq. units
Area of the triangle formed by the tangent and normal at (1, 1) on the curve and the y-axis is
Area bounded by the curve and area bounded by latus rectum of
The area of the part of circle x2 + y2 - 2x - 4y -1 = 0 above 2x - y = 0 is ...... sq. units
The area bounded by the curves y = |x| – 1 and y – |x| 1is
Area of closed curve 3(x -1)2 + 4(y2 - 3) = 0 is where [.] is G.I.F
Let f(x) = x + sin x. The area bounded by y = f-1 (x), y = x, x ∈ [0, π] is
The area of the region bounded by the curves |x + y| < 2, |x – y| < 2 and 2x2 + 6y2 > 3 is
Area enclosed by the closed curve 5x2 + 6xy + 2y2 + 7x + 6y + 6 = 0 is
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|

















