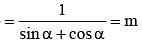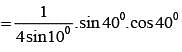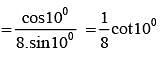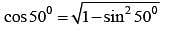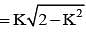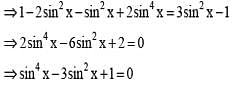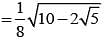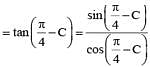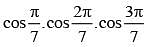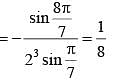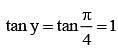JEE Advanced Level Test: Fundamentals of Trigonometric - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced Level Test: Fundamentals of Trigonometric
The maximum value of (cos α1), (cos α2),........(cos αn) under the restrictions 0 < α1, α2,....... and (cot α1), (cot α2),..........(cot αn) = 1 is
and (cot α1), (cot α2),..........(cot αn) = 1 is
 and (cot α1), (cot α2),..........(cot αn) = 1 is
and (cot α1), (cot α2),..........(cot αn) = 1 isThe number of integral values of k for which the equation 7 cos x + 5 sin x = 2k + 1 has a solution, is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If cos θ 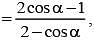 then tan θ/2 equals
then tan θ/2 equals
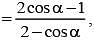 then tan θ/2 equals
then tan θ/2 equalsThe value of sin310o + sin350o - sin370o is equal to
Let n be a positive integer such that
If sin θ + sin 2θ + sin 3θ = sin α and cos θ + cos 2θ + cos 3θ = cos α , then θ is equal to
If π/2 < α < π and 3π/2 < β < 2π , sinα = 15/17 and tanβ =  , then sin (β - α) is
, then sin (β - α) is
If tan x + tan (x + π/3) + tan (x + 2π/3) = 3, then
If sin A = sin B and cos A = cos B, A > B, then
In a triangle ABC if A = π/4 and tanB tanC = K, then K must satisfy.
The number of pairs (x, y) satisfying the equations sin x + sin y = sin (x + y) and |x| + |y| = 1 is
If θ = 2π/7, then the value of tan θ tan 2θ + tan 2θ tan 4θ + tan 4θ tan θ is
Let A/2 = -140° then the value of
If sin2 (θ - α) cos α = cos2 (θ - α) sin α = m sin α cos α then
1 + sec 200 = cot x0.cot y0 then x+y may be
cos100.cos 200.cos 400 is equal to
If cos 250 + sin 250 = K, then cos 500 is equal to
If cos x = tan y, cos y = tan z, cos z = tan x then the value of sin x is
Which of the following is rational ?
If α + β + γ = π and tan  then the value of cos α + cos β + cos γ is
then the value of cos α + cos β + cos γ is
If sin x + cosec x + tan y + cot y = 4 where x and then tan y/2 is a root of the equation
If circumference of a circle is divided into 360 congruent parts, angle subtended by one part at center of circle is called
cot B = 2 tan A - B) ⇒ 2 tan B + cot B =
If log1/3 (5x – 1) > 0 then x belongs to
|
447 docs|930 tests
|
|
447 docs|930 tests
|


 [sin 2α1. sin2α2 .........sin 2αn]
[sin 2α1. sin2α2 .........sin 2αn]
 < a sinx + bcos x
< a sinx + bcos x 
 7cosx+5sinx
7cosx+5sinx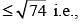



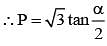


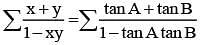
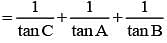





 is equal to
is equal to 


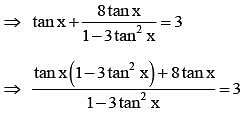

 ...........(1)
...........(1) ..........(2)
..........(2)