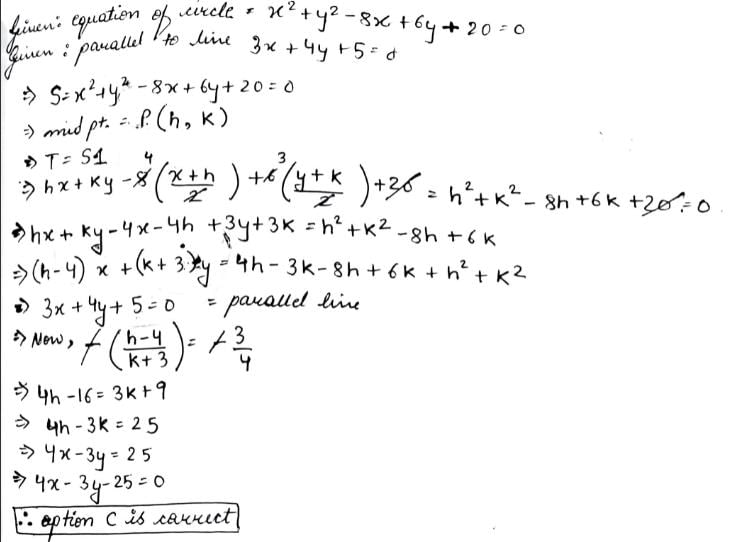Test: Circle- 3 - JEE MCQ
30 Questions MCQ Test - Test: Circle- 3
Find the equation of the circle passing through (–2, 14) and concentric with the circle x2 + y2 - 6x - 4y -12 = 0.
Centre and radius of the circle with segment of the line x + y = 1 cut off by coordinate axes as diameter is
The length of the tangent from (1, 1) to the circle 2x2 + 2y2 + 5x + 3y + 1 = 0 is
Slopes of tangents through (7, 1) to the circle x2 + y2 = 25 satisfy the equation
The centre of the circle passing through origin and making intercepts 8 and –4 on x and y axes respectively is
Equation of circles touching x-axis at the origin and the line 4x – 3y + 24 = 0 are
The equation of the chord of x2 + y2 - 4x + 6y + 3 = 0 whose mid point is (1, -2) is
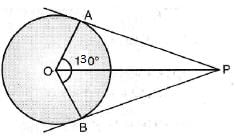
In the given figure, PA and PB are tangents from P to a circle with centre O. If ∠AOB = 130°, then find ∠APB.
If the two circles (x - 1)2 + (y - 3)2 = r2 and x2 + y2 - 8x + 2y + 8 = 0 intersect in two distinct points, then
If the distance between the centres of two circles of radii 3, 4 is 25 then the length of the transverse common tangent is
The equation of the tangent to the circle x2 + y2 - 4x + 4y - 2 = 0 and (1, 1) is
Equation of the tangent to the circle x2 + y2 - 2x + 4y - 4 = 0 which is parallel to the line 3x + 4y -1 = 0 is
The equation to the side BC of ΔABC is x + 5 = 0. If (-3, 2) is the orthocentre and (0, 0) is the circumcentre then radius of the circle is
The chord of contact of (1, 2) with respect to the circle x2 + y2 - 4x - 6y + 2 = 0 is
The circles x2 + y2 - 8x + 6y + 21 = 0 , x2 + y2 + 4x - 10y - 115 = 0 ar
If the circles x2 + y2 + 2gx + 2fy = 0 x2 + y2 + 2g' x + 2f ' y = 0 touch each other then
Locus of the point of intersection of tangents to the circle. x2 + y2 + 2x + 4y - 1 = 0 which include an angle of 60o is
Number of circles touching all the lines x + y – 1 = 0, x – y – 1 = 0 and y + 1 = 0 are
If the line y = x touches the circle x2 + y2 + 2gx + 2fy + c = 0 at P where OP = 6√2 then c =
If the tangent at (3, –4) to the circle x2 + y2 - 4x + 2y - 5 = 0 cuts the circle x2 + y2 + 16x + 2y + 10 = 0 in A and B then the mid point of AB is
Locus of mid points of chords to the circle x2 + y2 - 8x + 6y + 20 = 0 which are parallel to the line 3x + 4y + 5 = 0 is
If the circles x2 + y2 = 2 and x2 + y2 - 4x - 4y + λ = 0 have exactly three real common tangents then λ =
The locus of midpoints of chords of the circle x2 + y2 - 2x - 2y - 2 = 0 which make an angle of 120o at the centre is
If P and Q are the points of intersection of the circles x2 + y2 + 3x + 7y + 2p - 5 = 0 and x2 + y2 + 2x + 2y - p2 = 0 , then there is a circle passing through P, Q and (1, 1) for
Lengths of common tangents of the circles x2 + y2 = 6x, x2 + y2 + 2x = 0 are
The centre of the circle passing through the points (0, 0), (1, 0) and touching the circle x2 + y2 = 9 is
The line 2x – y + 1 = 0 is tangent to the circle at the point (2, 5) and the centre of the circles lies on x – 2y = 4. The radius of the circle is
Circle with centre (0, 4) and passing through the projection of (2, 4) on x-axis is