Test: Comprehension Based Questions: Definite Integrals and Applications of Integrals - JEE MCQ
16 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: Comprehension Based Questions: Definite Integrals and Applications of Integrals
Let the definite integral be defined by the formula 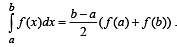 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 
Q. 
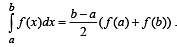 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 

Let the definite integral be defined by the formula 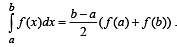 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 
Q.  then f(x) is of maximum degree
then f(x) is of maximum degree
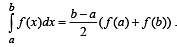 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 
 then f(x) is of maximum degree
then f(x) is of maximum degree| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let the definite integral be defined by the formula 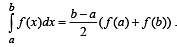 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 
Q.  and c is a point such that a < c < b, and (c, f(c)) is the point lying on the curve for which F(c) is maximum, then f '(c) is equal to
and c is a point such that a < c < b, and (c, f(c)) is the point lying on the curve for which F(c) is maximum, then f '(c) is equal to
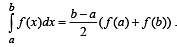 For more accurate result for c ∈ (a, b), we can use
For more accurate result for c ∈ (a, b), we can use  that for
that for 
 and c is a point such that a < c < b, and (c, f(c)) is the point lying on the curve for which F(c) is maximum, then f '(c) is equal to
and c is a point such that a < c < b, and (c, f(c)) is the point lying on the curve for which F(c) is maximum, then f '(c) is equal toPASSAGE - 2
Consider the functions defined implicitly by the equation y3 – 3y + x = 0 on various intervals in the real line. If x ∈(-∞, - 2) ∪ (2,∞) , the equation implicitly defines a unique real valued differentiable function y = f (x). If x ∈(-2, 2) , the equation implicitly defines a unique real valued differentiable function y = g(x) satisfying g(0) = 0.
Q. 
PASSAGE - 2
Consider the functions defined implicitly by the equation y3 – 3y + x = 0 on various intervals in the real line. If x ∈(-∞, - 2) ∪ (2,∞) , the equation implicitly defines a unique real valued differentiable function y = f (x). If x ∈(-2, 2) , the equation implicitly defines a unique real valued differentiable function y = g(x) satisfying g(0) = 0.
Q. The area of the region bounded by the curve y = f (x), the x-axis, and the lines x = a and x = b, where -∞ < a <b <-2 , is
PASSAGE - 2
Consider the functions defined implicitly by the equation y3 – 3y + x = 0 on various intervals in the real line. If x ∈(-∞, - 2) ∪ (2,∞) , the equation implicitly defines a unique real valued differentiable function y = f (x). If x ∈(-2, 2) , the equation implicitly defines a unique real valued differentiable function y = g(x) satisfying g(0) = 0.
Q. 
PASSAGE - 3
Consider the function f : ( -∞,∞) →(-∞,∞) defined by

Q. Which of the following is true?
PASSAGE - 3
Consider the function f : ( -∞,∞) →(-∞,∞) defined by

Q. Which of the following is true?
PASSAGE - 3
Consider the function f : ( -∞,∞) →(-∞,∞) defined by

Q.  Which of the following is true?
Which of the following is true?
PASSAGE - 4
f (x) = 1 + 2x + 3x2 + 4x3.
Let s be the sum of all distinct real roots of f (x) and let t = |s|.
Q. The real numbers lies in the interval
PASSAGE - 4
f (x) = 1 + 2x + 3x2 + 4x3.
Let s be the sum of all distinct real roots of f (x) and let t = |s|.
Q. The area bounded by the curve y = f (x) and the lines x = 0, y = 0 and x = t, lies in the interval
PASSAGE - 4
f (x) = 1 + 2x + 3x2 + 4x3.
Let s be the sum of all distinct real roots of f (x) and let t = |s|.
Q. The function f'(x) is
PASSAGE - 5
Given that for each  dt exists. Let this limit be g(a). In addition, it is given that the function g(a) is differentiable on (0, 1).
dt exists. Let this limit be g(a). In addition, it is given that the function g(a) is differentiable on (0, 1).
Q. The value of 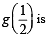
PASSAGE - 5
Given that for each  dt exists. Let this limit be g(a). In addition, it is given that the function g(a) is differentiable on (0, 1).
dt exists. Let this limit be g(a). In addition, it is given that the function g(a) is differentiable on (0, 1).
Q. 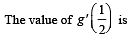
PASSAGE - 6
 be a thrice differentiable function. Suppose that F(1) = 0, F(3) = –4 and F(x) < 0 for
be a thrice differentiable function. Suppose that F(1) = 0, F(3) = –4 and F(x) < 0 for 

Q. The correct statement(s) is(are)
PASSAGE - 6
 be a thrice differentiable function. Suppose that F(1) = 0, F(3) = –4 and F(x) < 0 for
be a thrice differentiable function. Suppose that F(1) = 0, F(3) = –4 and F(x) < 0 for 

Q. 
|
347 docs|185 tests
|
|
347 docs|185 tests
|


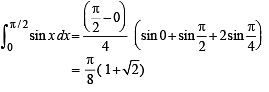





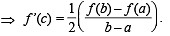













 and hence
and hence 











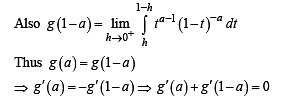

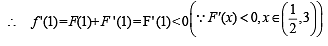

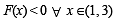


 ...(i)
...(i)
















