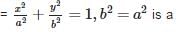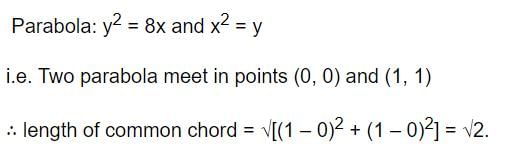Test: Conic Sections - 2 - JEE MCQ
25 Questions MCQ Test - Test: Conic Sections - 2
The radius of the circle passing through the foci of the ellipse 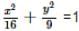 and having its centre at (0, 3) is
and having its centre at (0, 3) is
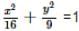 and having its centre at (0, 3) is
and having its centre at (0, 3) isThe line y = c is a tangent to the parabola 7/2 if c is equal to
The locus of a variable point whose distance from the point (2, 0) is 2/3 times its distance from the line x = 9/2 is
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is
Locus of the point of intersection of the lines x = sec θ + tan θ and y = sec θ – tan θ is
The two parabolas x2 = 4y and y2 = 4x meet in two distinct points. One of these is the origin and the other is
The equation of the directrix of the parabola x2 = −4ay is
The equations x = a cos θ , y = b sin θ, 0 ≤ θ < 2π , a ≠ b, represent
The graph of the function f(x) i/x i.e. the curve y = 1/x is
The lngth of the common chord of the parabolas y2 = x and x2 = y is
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is
The angle between the tangents drawn from the origin to the circle = (x−7)2+(y+1)2 = 25 is





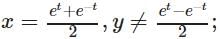 t ∈ R represents
t ∈ R represents