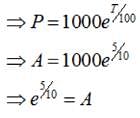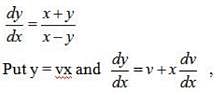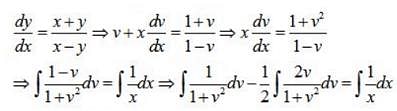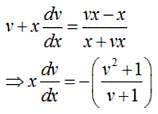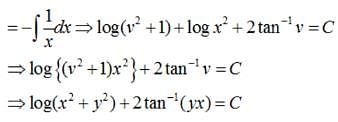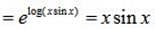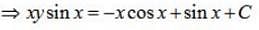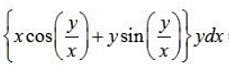Test: Differential Equations- 2 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Differential Equations- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs1000 is deposited with this bank, how much will it worth after 10 years (e0.5= 1.648).
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).
General solution of sec2 x tany dx + sec2y tan x dy = 0 is
Find the particular solution for (x + y) dy + (x –y) dx = 0; y = 1 when x = 1
Variable separation method can be used to solve First Order, First Degree Differential Equations in which y’ is of the form.
Determine order and degree (if defined) of y’ + 5y = 0
General Solution of (ex + e-x) dy - (ex - e-x) dx = 0
solution of {x cos (y/x) + ysin(y/x)} ydx = {ysin(y/x) - x cos (y/x)} xdy is
To form a differential equation from a given function
A differential equation of the form y' = F(x,y) is homogeneous if
General solution of(1+x2) dy+2xy dx = cot x dx(x ≠ 0) is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|