Test: Differential Equations- Assertion & Reason Type Questions - JEE MCQ
6 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Differential Equations- Assertion & Reason Type Questions
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The differential equation formed by eliminating a and b from

Reason (R):y = aex + be-x ….(i)Differentiating w. r. t. 'x'
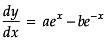
Differentiating again w .r .t .'x'
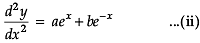
Subtracting eqn. (i) from eqn. (ii)
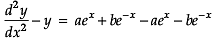
= 0
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The solution of differential equation
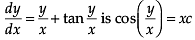
Reason (R): 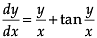 we can clearly see that it is an homogeneous equation substituting
we can clearly see that it is an homogeneous equation substituting
y = vx
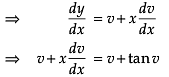
separating the variables and integrating we get
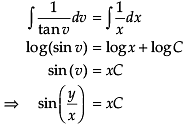
is the solution where, C is constant.
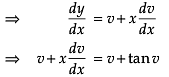
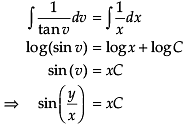
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The degree of the differential equation given by
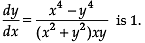
Reason (R): The degree of a differential equation is the degree of the highest order derivative when differential coefficients are free from radicals and fraction.
The given differential equation has first order derivative which is free from radical and fraction with power = 1, thus it has a degree of 1.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The order and degree of the differential equation  are 2 and 1
are 2 and 1
respectively
Reason (R): The differential equation

is of order 1 and degree 3.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): Solution of the differential equation
![]()
Reason (R):

separating the variables
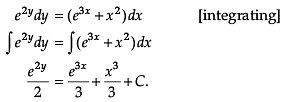
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The order of the differential equation given by ![]()
Reason (R): Since the order of a differential equation is defined as the order of the highest derivative occurring in the differential equation, i.e., for nth derivative dny/dxn if n = 1. then it’s order = 1.
Given differential equation contains only dy/dx derivative with variables and constants.
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|




















