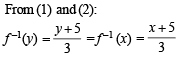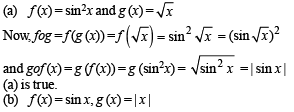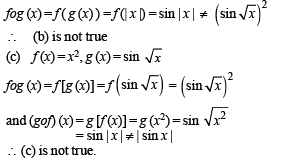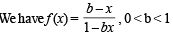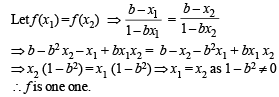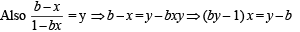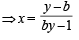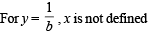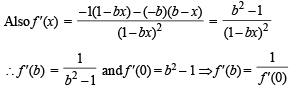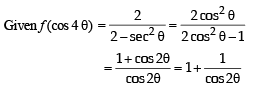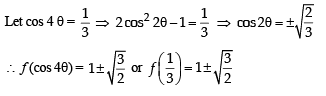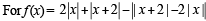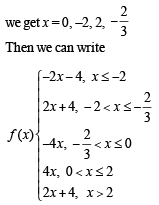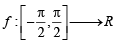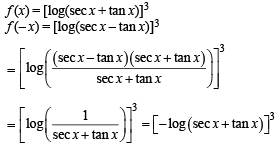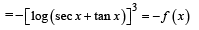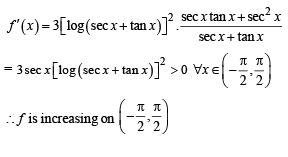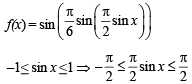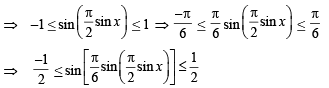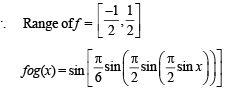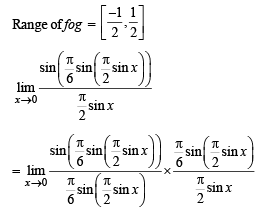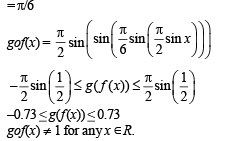Test: JEE Advanced (One or More Correct Option): Functions - Airforce X Y / Indian Navy SSR MCQ
11 Questions MCQ Test Mathematics for Airmen Group X - Test: JEE Advanced (One or More Correct Option): Functions
Let g (x) be a function defined on [– 1, 1]. If the area of the equilateral triangle with two of its vertices at (0,0) and 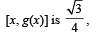 then the function g(x) is
then the function g(x) is
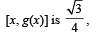 then the function g(x) is
then the function g(x) is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
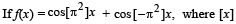 stands for the greatest integer function, then
stands for the greatest integer function, then
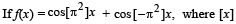 stands for the greatest integer function, then
stands for the greatest integer function, thenIf f(x) = 3x – 5, then f–1(x)
If g (f(x)) = | sin x | and f (g(x)) = (sin √x)2, then
Let f : (0, 1) → R be defined by 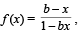 where b is a constant such that 0 < b < 1. Then
where b is a constant such that 0 < b < 1. Then
Let f : (–1, 1) ⇒ IR be such that 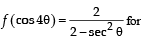
 Then the value (s) of
Then the value (s) of 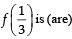
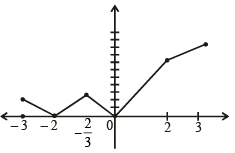
The function f(x) = 2|x| + |x + 2| – | |x + 2| – 2 |x| has a local minimum or a local maximum at x =
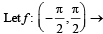 R be given by f (x) = (log(sec x + tan x))3.
R be given by f (x) = (log(sec x + tan x))3.
Then
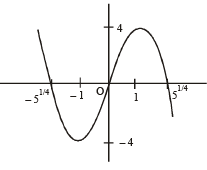
Let a ∈ R and let f : R → R be given by f (x) = x5 – 5x + a. Then
Let 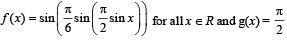 sin x for all x ∈ R. Let (fog)(x) denote f(g(x)) and (gof)(x) denote g(f(x)). Then which of the following is (are) true?
sin x for all x ∈ R. Let (fog)(x) denote f(g(x)) and (gof)(x) denote g(f(x)). Then which of the following is (are) true?
|
149 videos|192 docs|197 tests
|
|
149 videos|192 docs|197 tests
|


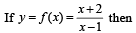
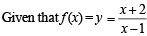
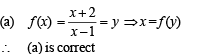
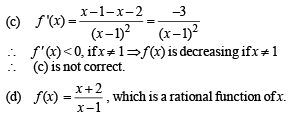
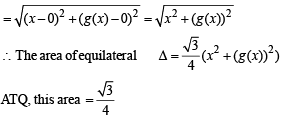
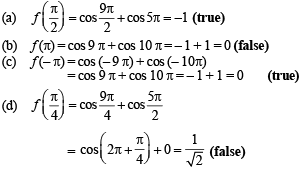
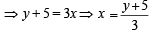 ...(1)
...(1)