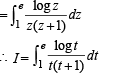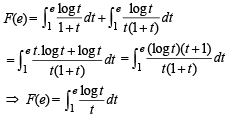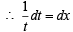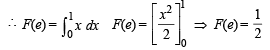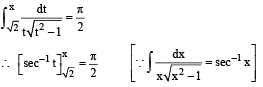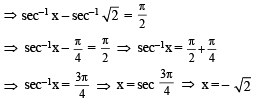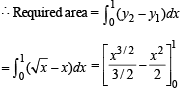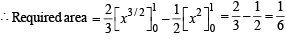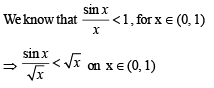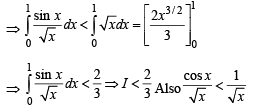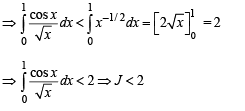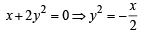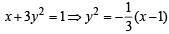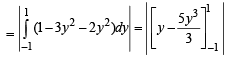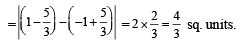Test: JEE Main 35 Year PYQs- Definite Integrals & Applications of Integrals - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - Test: JEE Main 35 Year PYQs- Definite Integrals & Applications of Integrals
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If y = f(x) makes +ve intercept of 2 and 0 unit on x and y axes and encloses an area of 3/4 square unit with the axes then
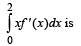
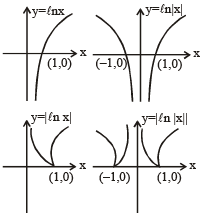
The area bounded by the curves y = lnx, y = ln |x|,y=| ln x | and y = | ln |x| | is
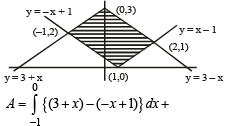
The area of the region bounded by the curves y = |x - 1| and y = 3 - |x| is
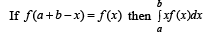 is equal to
is equal to
Let f(x) be a function satisfying f '(x) = f(x) with f(0) = 1 and g(x) be a function that satisfies f(x) + g(x) = x2 . Then the value of the integral 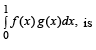
The value of the integral 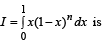

and 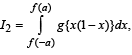 then the value of
then the value of 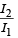 is
is
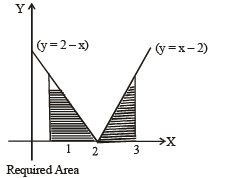
The area of the region boun ded by the curves y = | x - 2 |, x = 1,x = 3 and the x-axis is
The area enclosed between the curve y = loge (x +e) and the coordinate axes is
The parabolas y2 = 4x and x2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes. If S1 , S2 , S3 are respectively the areas of these parts numbered from top to bottom; then S1 : S2 : S3 is
Let f (x) be a non – negative continuous function such that the area bounded by the curve y = f (x), x - axis and the
ordinates 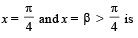
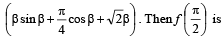
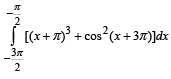 is equal to
is equal to
The value of 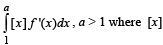 denotes the greatest integer not exceeding x is
denotes the greatest integer not exceeding x is
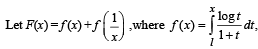 Then F(e) equals
Then F(e) equals
The solution for x of the equation 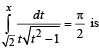
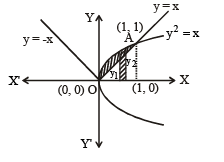
The area enclosed between the curves y2 = x and y = | x | is
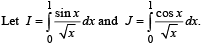 Then which one of the following is true?
Then which one of the following is true?
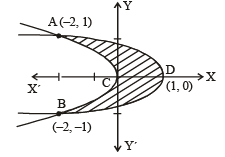
The area of the plane region bounded by the curves x + 2y2 = 0 and x + 3y2 = 1is equal to
|
149 videos|192 docs|197 tests
|
|
149 videos|192 docs|197 tests
|


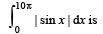
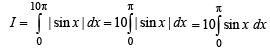
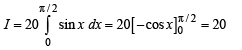
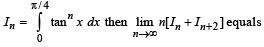
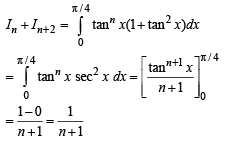
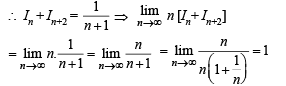
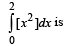
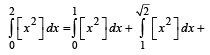
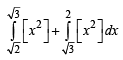
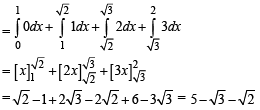
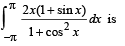
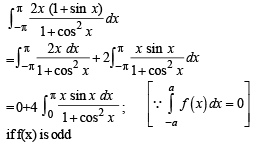
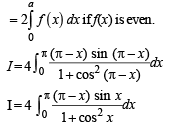
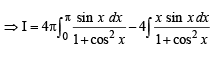
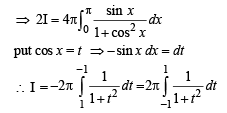
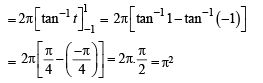
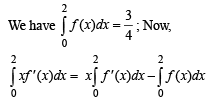
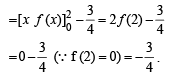

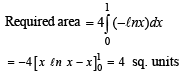
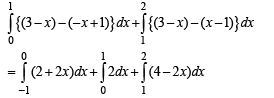
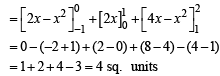
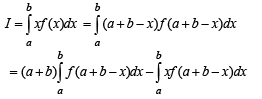
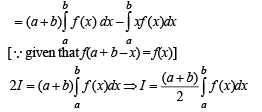
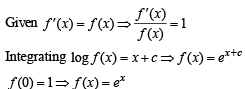
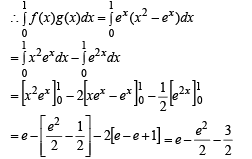
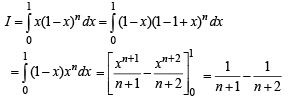
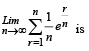
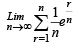 [Using definite integrals as limit of sum]
[Using definite integrals as limit of sum]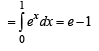
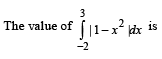
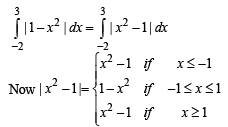
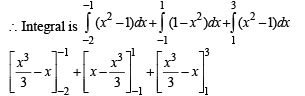
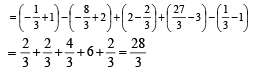
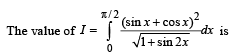
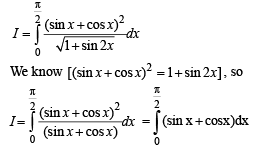
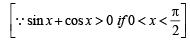
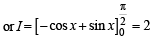
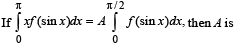
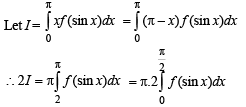

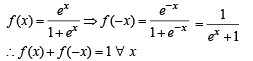
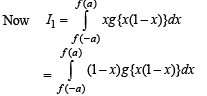
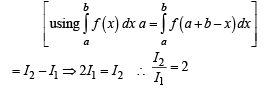
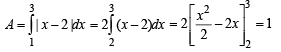
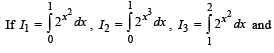
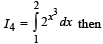
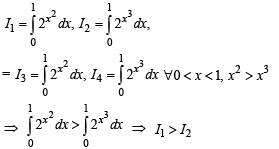
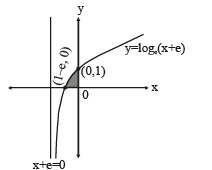
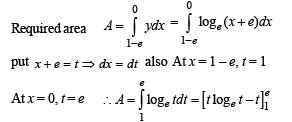
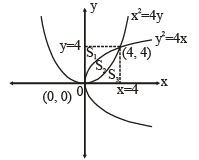
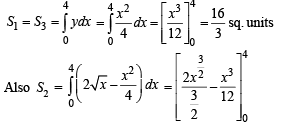
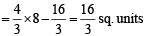

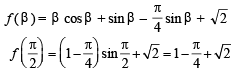
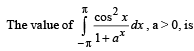
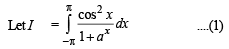

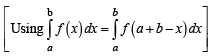

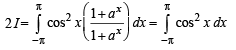
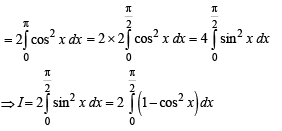
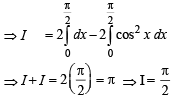
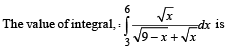
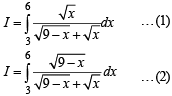
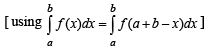
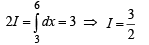

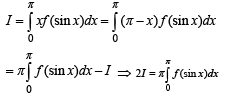
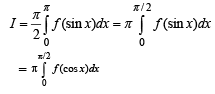
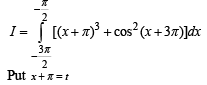
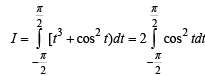
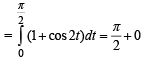
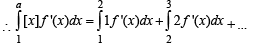
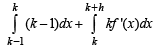
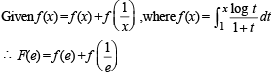
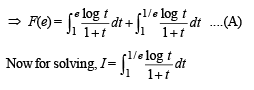
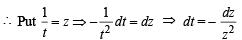
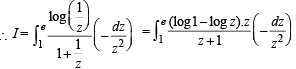
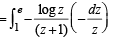 [∴ log1 = 0]
[∴ log1 = 0]