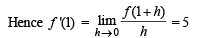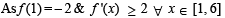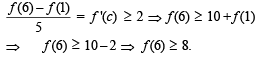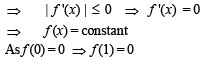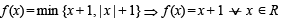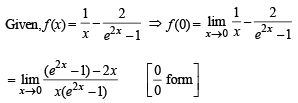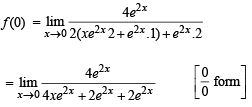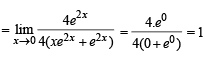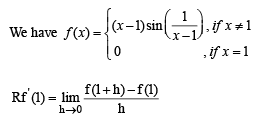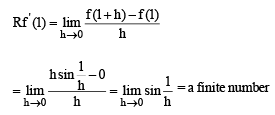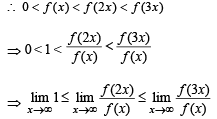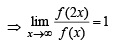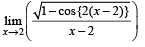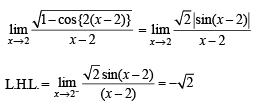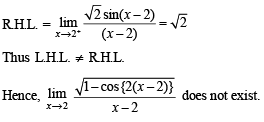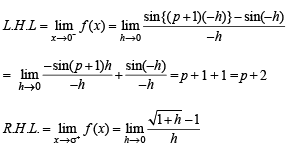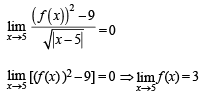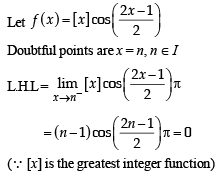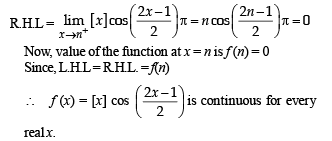Test: JEE Main 35 Year PYQs- Limits, Continuity & Differentiability - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - Test: JEE Main 35 Year PYQs- Limits, Continuity & Differentiability
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let f (x) = 4 and f ' (x) = 4. Then 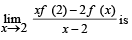 given by
given by
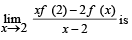 given by
given by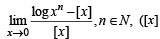 denotes greatest integer less than or equal to x)
denotes greatest integer less than or equal to x)
If f(1) = 1, f 1 (1) = 2, then 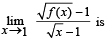
f is defined in [-5, 5] as f(x) = x if x is rational = –x if x is irrational. Then
f(x) and g(x) are two differentiable functions on [0, 2] such that f ''( x) - g '' (x)= 0, f ' (1) =2g'(1)=4 f(2) =3g(2) = 9 then f(x)–g(x) at x = 3/2 is
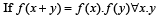 and f (5) = 2,f '(0)= 3 , then f ' (5) is
and f (5) = 2,f '(0)= 3 , then f ' (5) is
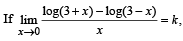 the value of k is
the value of k is
Let f (a) = g (a) = k and their nth derivatives
fn (a) , gn (a) exist and are not equal for some n. Further if
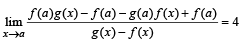
then the value of k is
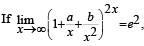 then the values of a and b, are
then the values of a and b, are
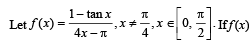 is continuous
is continuous 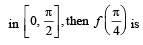
Let a and b be the distinct roots of ax2 + bx +c = 0 , then 
Suppose f(x) is differentiable at x = 1 and 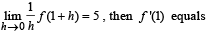
Let f be differentiable for all x. If f (1) = – 2 and f '(x) > 2 for x ∈ [1, 6], then
If f is a real valued differentiable function satisfying
|f (x) – f (y) | < ( x -y)2 , x, y ∈ R and f (0) = 0, then f (1) equals
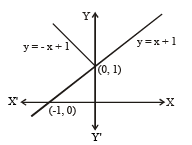
Let f : R → R be a function defined by f (x) = min {x + 1,x+ 1} ,Then which of the following is true ?
The function f : R /{0} → R given by
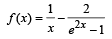
can be made continuous at x = 0 by defining f (0) as
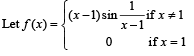
Then which one of the following is true?
Let f : R →R be a positive incr easing function with 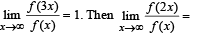
The values of p and q for which the function
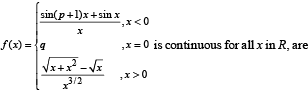
Let f : R → [0, ∞) be such that 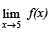 exists and
exists and 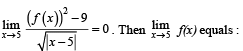
If f : R → R is a function defined by f (x) = [x] 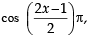 where [x] denotes the greatest integer function, then f is .
where [x] denotes the greatest integer function, then f is .
|
149 videos|192 docs|197 tests
|
|
149 videos|192 docs|197 tests
|


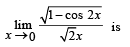
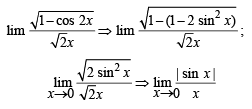
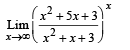
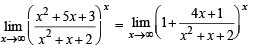
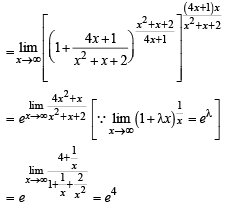
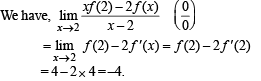
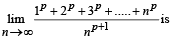
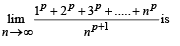
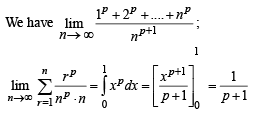
 does not exist, hence the required limit
does not exist, hence the required limit form using L’ Hospital’s rule
form using L’ Hospital’s rule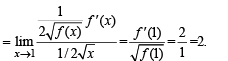

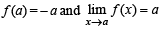
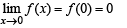

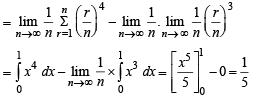

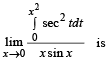
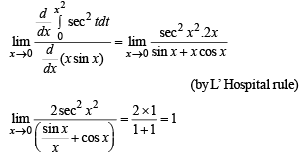
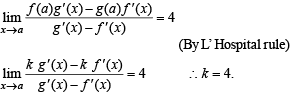
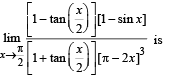
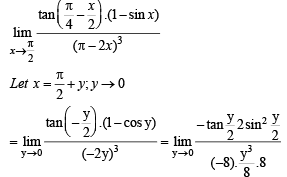
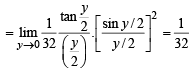
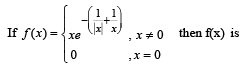
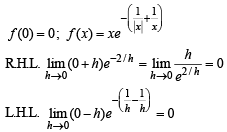
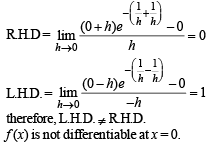
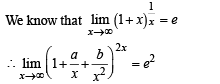
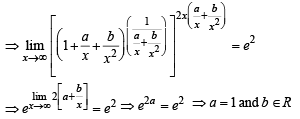
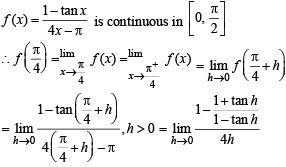
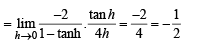
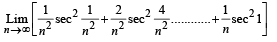 equals
equals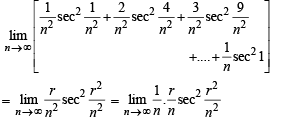
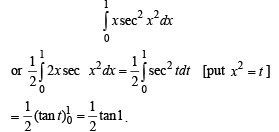
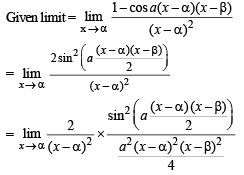
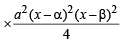
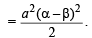

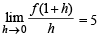 and hence f (1) = 0
and hence f (1) = 0