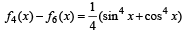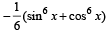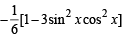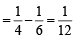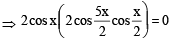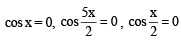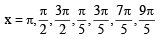Test: JEE Main 35 Year PYQs- Trigonometric Functions & Equations - Airforce X Y / Indian Navy SSR MCQ
16 Questions MCQ Test Mathematics for Airmen Group X - Test: JEE Main 35 Year PYQs- Trigonometric Functions & Equations
The period of sin2θ is [2002]
The number of solution of tan x + sec x = 2cos x in [0, 2π) is [2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one is not periodic [2002]
Let a, b be such that p < a - b < 3p. If 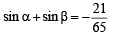 and
and 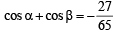 then the value of
then the value of 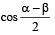 [2004]
[2004]
If 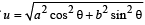
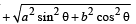 then the difference between the maximum and minimum values of u2 is given by [2004]
then the difference between the maximum and minimum values of u2 is given by [2004]
A line makes the same angle θ, with each of the x and z axis.
If the angle β, which it makes with y-axis, is such that sin 2β = 3 sin 2θ, then cos2θ equals [2004]
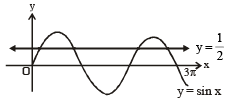
The number of values of x in the interval [0, 3π] satisfying the equation 2 sin 2 x + 5 sinx - 3 =0 is [2006]
If 0 < x < π and cosx + sin x = 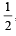 , then tan x is [2006]
, then tan x is [2006]
Let A and B denote the statements A : cosα + cosβ + cosγ = 0 B : sinα + sinβ + sinγ = 0
If cos (β – γ) + cos (γ – α) + cos (α – β) =  then : [2009]
then : [2009]
Let 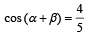 and sin
and sin 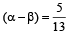 where
where  Then tan 2α = [2010]
Then tan 2α = [2010]
If A = sin2 x + cos4x, then for all real x : [2011]
In a ΔPQR, If 3 sin P + 4 cos Q = 6 and 4 sin Q + 3 cos P = 1, then the angle R is equal to : [2012]
A B C D is a trapezium such that A B and CD are parallel and BC ⊥ CD. If ΔADB = θ, BC = p and CD = q, then AB is equal to : [JEE M 2013]
The expression 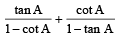 can be written as :[JEE M 2013]
can be written as :[JEE M 2013]
Let 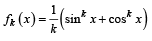 where x ∈ R and k ≥ 1.Then f4 (x) - f6 (x) equals [JEE M 2014]
where x ∈ R and k ≥ 1.Then f4 (x) - f6 (x) equals [JEE M 2014]
If 0 ≤ x < 2p, then the number of real values of x, which satisfy the equation cos x + cos 2x + cos 3x + cos 4x = 0 is: [JEE M 2016]
|
149 videos|192 docs|197 tests
|
|
149 videos|192 docs|197 tests
|


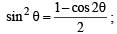 ; Period
; Period 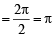
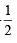 , –1.;
, –1.;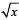 is non periodic
is non periodic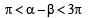

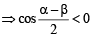
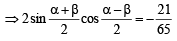 .....(1)
.....(1)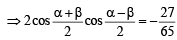 .....(2)
.....(2)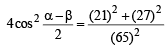
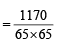
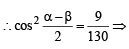
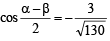
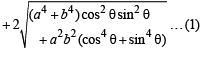
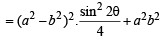 …(2)
…(2)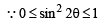
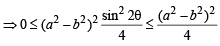
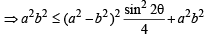
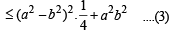
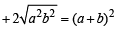
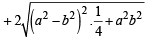
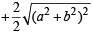 = 2(a 2+b2)
= 2(a 2+b2)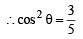
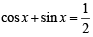
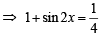
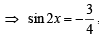 ⇒ 3 tan 2 x + 8 tanx + 3= 0
⇒ 3 tan 2 x + 8 tanx + 3= 0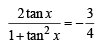 ⇒ 3 tan 2 x + 8 tanx + 3= 0
⇒ 3 tan 2 x + 8 tanx + 3= 0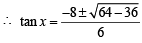
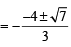
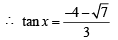

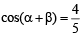
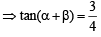
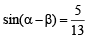
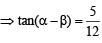
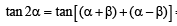
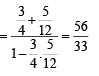
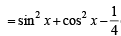
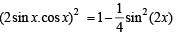
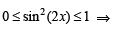
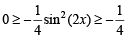
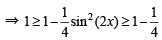
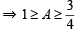
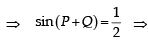
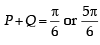
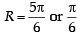 (∵P + Q + R = p)
(∵P + Q + R = p)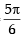 then 0 < P,Q <
then 0 < P,Q < 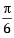
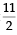 which is not true.
which is not true.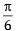
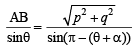
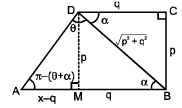
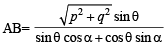
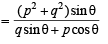
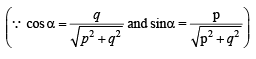
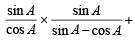
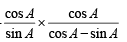
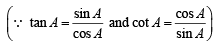
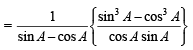
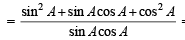 = 1 + sec A cosec AA
= 1 + sec A cosec AA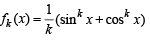 Consider
Consider