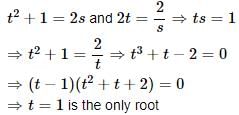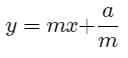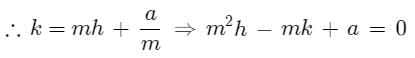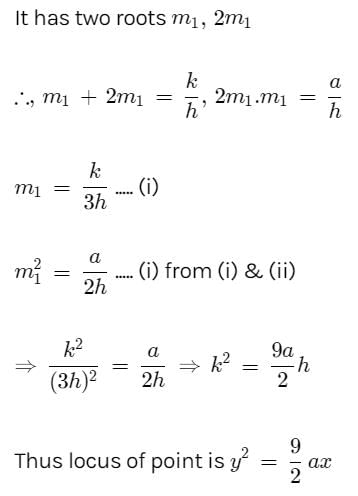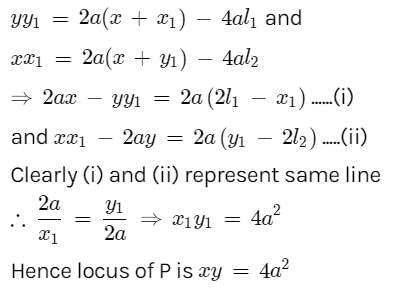Test: Parabola - 2 - JEE MCQ
20 Questions MCQ Test - Test: Parabola - 2
If the line x + y – 1 = 0 touches the parabola y2 = kx , then the value of k is
Directrix of a parabola is x + y = 2. If it's focus is origin, then latus rectum of the parabola is equal to
Which one of the following equations represents parametrically, parabolic profile ?
If (t2, 2t) is one end of a focal chord of the parabola y2 = 4x then the length of the focal chord will be
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is
The point of intersection of the curves whose parametric equations are x = t2 + 1, y = 2t and x = 2s, y = 2/s is given by
PN is an ordinate of the parabola y2 = 4ax. A straight line is drawn parallel to the axis to bisect NP and meets the curve in Q. NQ meets the tangent at the vertex in a point T such that AT = kNP, then the value of k is (where A is the vertex)
The tangents to the parabola x = y2 + c from origin are perpendicular then c is equal to
The locus of a point such that two tangents drawn from it to the parabola y2 = 4ax are such that the slope of one is double the other is
T is a point on the tangent to a parabola y2 = 4ax at its point P. TL and TN are the perpendiculars on the focal radius SP and the directrix of the parabola respectively. Then
The equation of the circle drawn with the focus of the parabola (x – 1)2 – 8y = 0 as its centre and touching the parabola at its vertex is
The equation of the tangent at the vertex of the parabola x2 + 4x + 2y = 0 is
Locus of the point of intersection of the perpendicular tangents of the curve y2 + 4y – 6x – 2 = 0 is
Tangents are drawn from the points on the line x – y + 3 = 0 to parabola y2 = 8x. Then the variable chords of contact pass through a fixed point whose coordinates are
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are
If (3t12-6t1) represents the feet of the normals to the parabola y2 = 12x from (1, 2), then Σ1/t1 is
TP & TQ are tangents to the parabola, y2 = 4ax at P & Q. If the chord PQ passes through the fixed point (–a, b) then the locus of T is
If the tangent at the point P (x1, y1) to the parabola y2 = 4ax meets the parabola y2 = 4a (x + b) at Q & R, then the mid point of QR is
Let PSQ be the focal chord of the parabola, y2 = 8x. If the length of SP = 6 then, l(SQ) is equal to(where S is the focus)
Two parabolas y2 = 4a(x – l1) and x2 = 4a(y – l2) always touch one another, the quantities l1 and l2 are both variable. Locus of their point of contact has the equation