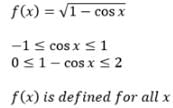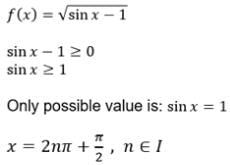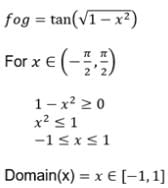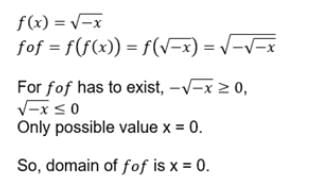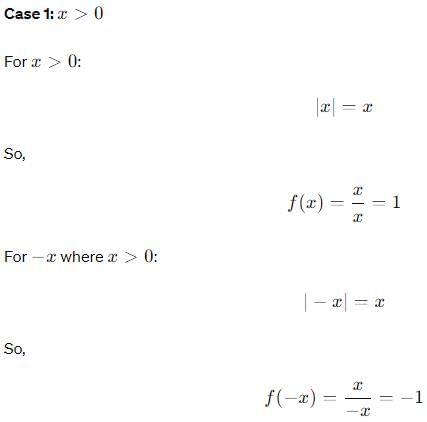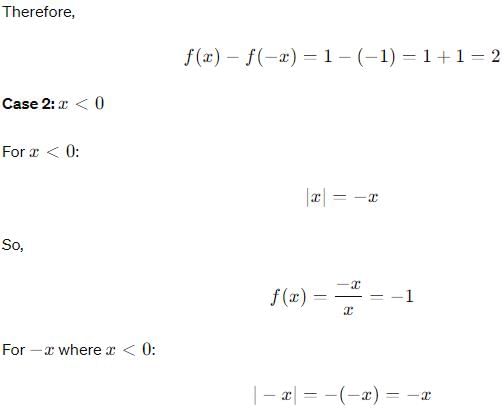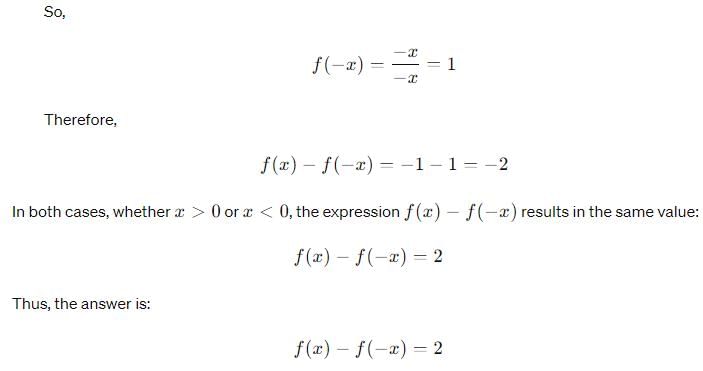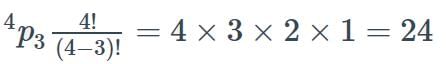Test: Relations & Functions- 3 - JEE MCQ
25 Questions MCQ Test - Test: Relations & Functions- 3
Let x be any real, then [x + y] = [x] + [y] holds for
A function / from the set of natural numbers to integers defined by
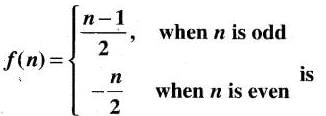
The interval in which the values of f (x) lie where f (x) = 3 sin
If the function f(x) is defined as
f(x) = { 2x - 3, for x ≥ 2
x, for x < 2
then what is the value of f(1)?
A condition for a function y = f (x) to have an inverse is that it should be
Set A has 3 elements and set B has 4 elements. The number of injections that can be defined from A to B is
On the set Z of all integers define f ; Z → Z as follows : f (x) = {x/2 if x is even, and f (x) = 0 if x is odd , then f is
Let f : R → R be defined by f (x) = 3x – 4, then f-1 (x) is equal to
The number of bijective functions from the set A to itself when A constrains 106 elements is
In the set W of whole numbers an equivalence relation R defined as follow : aRb iff both a and b leave same remainder when divided by 5. The equivalence class of 1 is given by


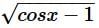 is
is