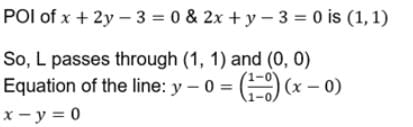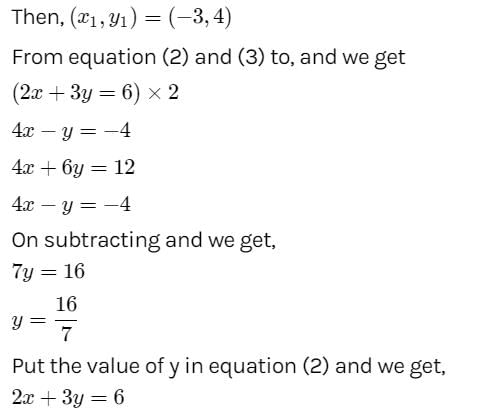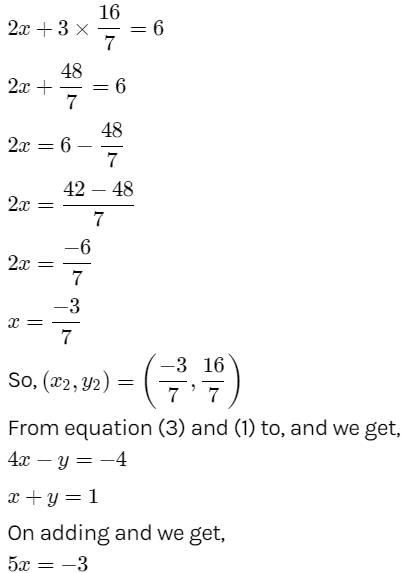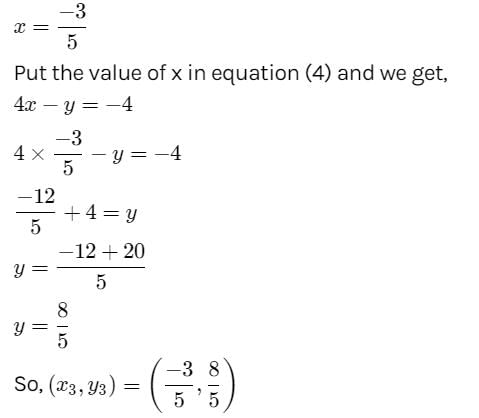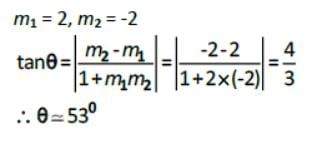Test: Straight Lines- 2 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Straight Lines- 2
The lines x + (k – 1) y + 1 = 0 and 2x+k2y−1 = 0 are at right angles if
A line is equally inclined to the axis and the length of perpendicular from the origin upon the line is √2. A possible equation of the line is
The lines y = mx , y + 2x = 0 , y = 2x + λ and y = - mx + λ form a rhombus if m =
Two points (a , 0) and (0 , b) are joined by a straight line. Another point on this line is
The coordinates of the foot of perpendicular from (0 , 0) upon the line x + y = 2 are
The area of the triangle whose sides are along the lines x = 0 , y = 0 and 4x + 5y = 20 is
A line is drawn through the points (3 , 4) and (5 , 6) . If the is extended to a point whose ordinate is – 1, then the abscissa of that point is
The line x + y – 6 = 0 is the right bisector of the segment [PQ]. If P is the point (4, 3) , then the point Q is
The acute angle between the lines ax + by + c = 0 and (a + b)x = (a – b)y, a ≠ b, is
The lines x + 2y – 3 = 0, 2x + y – 3 = 0 and the line l are concurrent. If the line I passes through the origin, then its equation is
The triangle formed by the lines x + y = 1, 2x + 3y – 6 = 0 and 4x – y + 4 = 0 lies in
The area of triangle formed by the lines y = x, y = 2x and y = 3x + 4 is
If the points representing the complex numbers - 4 +3i , 2 – 3i and 0 + π are collinear , then the value of p is
The lines ix + my + n = 0 , mx + ny + l = 0 and nx + ly +m = 0 are concurrent if
The equations of the lines through (- 1 , - 1) and making angles of 450 with the line x + y = 0 are
Given the 4 lines with equations x + 2y – 3 = 0, 2x + 3y – 4 = 0, 3x + 4y – 5 = 0, 4x + 5y – 6 = 0 , then these lines are
The orthogonal projection of the point (2 , - 3) on the line x + y = 0 is
Three points A , B and C are collinear if the area of triangle ABC is
The lines 8x + 4y = 1, 8x + 4y = 5, 4x + 8y = 3, 4x + 8y = 7 form a
The number of points on X axis which are at a distance of c units (c < 3) from (2 , 3) is
If (x , y) are the coordinates of point in the plane , then 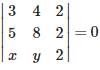 represents
represents
|
75 videos|238 docs|91 tests
|