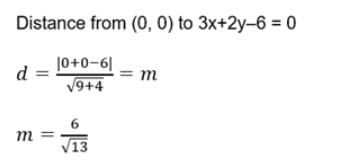Test: Distance Between Lines - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Distance Between Lines
If the length of the perpendicular from the origin to the line 3x+2y = 6 is m. What is the value of m?
What is the angle made by the perpendicular from the origin to the line x+ √3y = 2 with the positive direction of x axis?
The slope of a line is 3 and its y intercept is 2.What is the distance of such a line from the point (1,-2)?
What will be the co-ordinates of foot of perpendicular line drawn from the point (-1,3) to the line 3x-4y-16=0?
What is the distance of the point (3,3) from the line 2(x-3) = 3(y+5)?
What is the distance between the parallel lines 3(x+y) + 2 = 0 And 6x+6y+28 = 0?
The point on y-axis equidistant from the points (3,2) and (-1,3) is
A point P is in the interior of angle BAC, such that P lies on the bisector of angle BAC. What can be said about the distance of PM if PN = 2cm where PM and PN are perpendiculars from P on the lines BA and AC?
For a line whose equation is √3x + y = 8, the length of the perpendicular from the origin is
The distance between the parallel lines 4x-3y+5 = 0 and 4x-3y+15 = 0 is :
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|