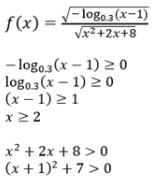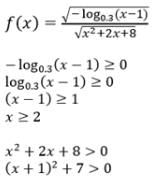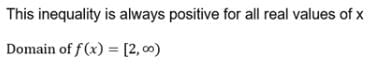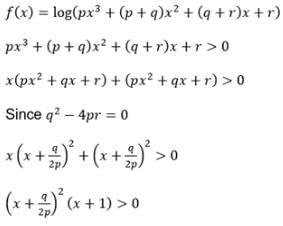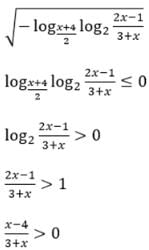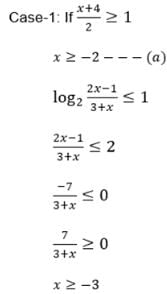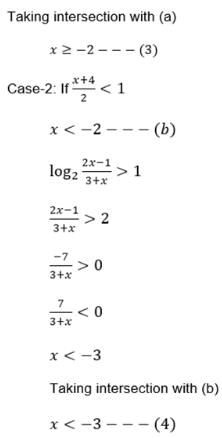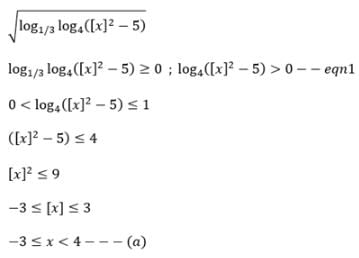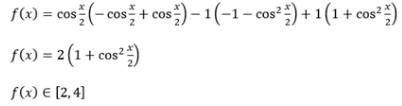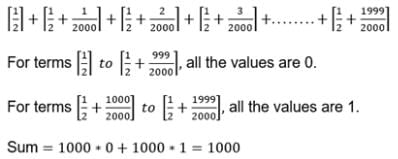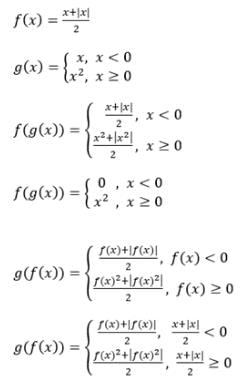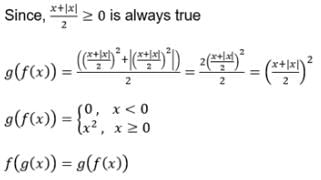JEE Advanced Level Test: Relations and Functions- 1 - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - JEE Advanced Level Test: Relations and Functions- 1
The domain of the function f(x)=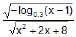 is
is
The domain of the function f(x) = log1/2 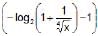 is
is
If q2 – 4pr = 0, p > 0, then the domain of the function, f(x) = log (px3 + (p + q) x2 + (q + r) x + r) is
Find domain of the function f(x) =
The domain of the function is (where [x] denotes greatest integer function)
Range of f(x) = 4x + 2x + 1 is
Range of f(x) = log√5 {√2 (sin x –cos x) + 3} is
The range of the functin f(x) = log√2(2– log2 (16 sin2 x + 1)) is
Range of the function f(x)= is
If f(x) = , then range of f(x) is
The sum is equal to (where [*] denotes the greatest integer function)
Which of the following represents the graph of f(x) = sgn ([x + 1])
If f(x) = 2 sin2q+4 cos (x+q) sin x. sin q+cos (2x+2q) then value of f2(x) + f2 is
Let f(x) = ax2 + bx + c, where a, b, c are rational and f : Z → Z, where Z is the set of integers. Then a+ b is
Which one of the following pair of functions are identical ?
The function f : [2, ∞) → Y defined by f(x) = x2 – 4x + 5 is both one–one & onto if
Let f : R → R be a function defined by f(x) = then f is
Let f : R → R be a function defined by f(x) = x3 + x2 + 3x + sin x. Then f is
If f(x) = x3 + (a – 3) x2 + x + 5 is a one–one function, then
The graph of the function y = f(x) is symmetrical about the line x = 2, then-
The function f : R → R defined by f(x) = 6x + 6|x| is
Let `f' be a function from R to R given by f(x) = . Then f(x) is
If f(x) = cot-1 x : R+ → and g(x) = 2x – x2 : R → R. Then the range of the function f(g(x)) wherever define is
Let g(x) = 1 + x – [x] and f(x) = , then
x, fog(x) equals (where [*] represents greatest integer function).
Let f: [0, 1] → [1, 2] defined as f(x) = 1 + x and g : [1, 2] → [0, 1] defined as g(x) = 2 – x then the composite function gof is
Let f & g be two functions both being defined from R → R as follows f(x) = and g(x) =
. Then
If y = f (x) satisfies the condition f = x2 +
(x > 0) then f(x) equals
It is given that f(x) is an even function and satisfy the relation f(x) = then the value of f(10) is
Fundamental period of f(x) = sec (sin x) is
|
149 videos|192 docs|197 tests
|