JEE Advanced Level Test: Relations and Functions- 3 - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - JEE Advanced Level Test: Relations and Functions- 3
The domain of f (x) = log | logx | is
The domain of the function 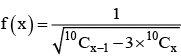 contains the points
contains the points
The range of the function f (x) = cot-1 (2x- x2) is
The function where [x] denotes the greatest integer less than or equal to x, is defined for all x ∈
The domain of the function greatest integer less than or equal to x, is
If f(x) = ax7 + bx3 + cx – 5; a, b, c are real constants and f (-7) = 7, then the range of f(7) + 17 cos x is
The domain of the function where {.} denotes the fractional part, is
The range of the function f defined by respectively, denote the greatest integer and the fractional part] is
Let f(x) 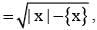 (where {.} denotes the fractional part of x and X, Y are its domain and range, respectively), then
(where {.} denotes the fractional part of x and X, Y are its domain and range, respectively), then
The domain of f(x) where {.} denotes the fractional part in [-1,1], is
The range of where [.] denotes the greater integer function, is
The domain of f(x) = sin -1 [2x2 - 3], where [.] denotes the greatest integer function, is
The range of f(x) = [|sin x |+| cos x|] , where [.] denotes the greatest integer function, is
The range of where [.] denote the greatest integer function £ x , is
Let A = {1, 2, 3} and let R = {(1, 1), (2, 2), (3, 3), (1, 3), (3, 2), (1, 2)}. Then R is
Let A = {a, b, c} and let R = {(a, a)(a, b), (b, a)}. Then, R is
Let A = {1, 2, 3} then total number of relations in
Let S be the set of all straight lines in a plane. Let R be a relation on S defined by a R b ⇔ a ⊥ b. Then, R is
Let S be the set of all real numbers and let R be a relation on S, defined by a R b ⇔ |a – b| < 1. Then, R is
Let W denote the words in the English dictionary. Define the relation R by R = {(x, y) ∈ W × W| the words x and y have at least one letter in common}. Then, R is
Let R = {(3, 3), (6, 6), (9, 9), (3,6), (3, 9), (9, 12), (3,12), (6, 12), (12, 12)}, be a relation on the set A = {3, 6, 9, 12} Then the relation is
Let R be a relation on the set A of ordered pairs of positive integers defined by (x, y)R(u, v) if and only if xv = yu, then
|
149 videos|192 docs|197 tests
|


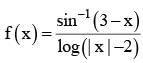

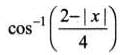
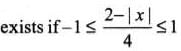
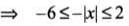
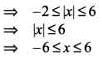
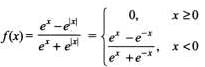
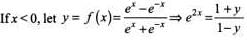
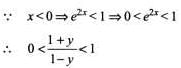
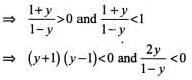
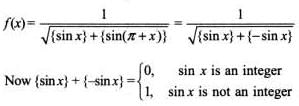
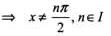
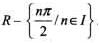

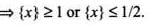
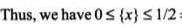
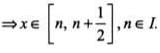
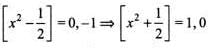
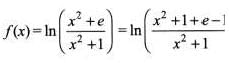
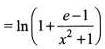
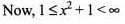
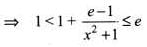
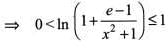
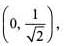
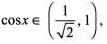
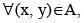 since xy = yx. This shows that R is reflexive.
since xy = yx. This shows that R is reflexive.














