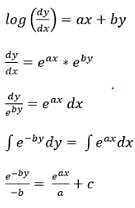JEE Advanced Level Test: Vector Algebra- 1 - JEE MCQ

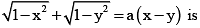
The differential equation of all parabolas whose axis are parallel to the y-axis is  

The differential equation of all circles which pass through the origin and whose centers lie on the y-axis is 

The differential equation whose general solution is given by, y =  , where c₁, c₂, c₃, c₄, c₅ are arbitrary constants, is 

The equation of the curves through the point (1, 0) and whose slope is 

The solution of the equation log(dy/dx) = ax + by is 

Solution of differential equation dy – sin x sin ydx = 0 is

The solution of the equation 

The general solution of the differential equation 

The solutions of (x + y + 1) dy = dx is

The slope of the tangent at (x, y) to a curve passing through  then the equation of the curve is 

The solution of (x² + xy)dy = (x² + y²)dx is 

The solution of (y + x + 5)dy = (y – x + 1) dx is 

The slope of the tangent at (x, y) to a curve passing through a point (2, 1) is  then the equation of the curve is 

The solution of  satisfying y(1) = 1 is given by 

Solution of the equation 

A function y = f(x) satisfies  then f(x) is 

The general solution of the equation 

The curve satisfying the equation  and passing through the point (4, - 2) is 

The solution of the differential equation 

Which of the following is not the differential equation of family of curves whose tangent from an angle of π/4 with the hyperbola xy = c²? 

Tangent to a curve intercepts the y-axis at a point P. A line perpendicular to this tangent through P passes through another point (1, 0). The differential equation of the curve is 

The curve for which the normal at any point (x, y) and the line joining the origin to that point from an isosceles triangle with the x-axis as base is

A normal at P(x, y) on a curve meets the x-axis at Q and N is the foot of the ordinate at P. If NQ =  then the equation of curve given that it passes through the point (3,1) is 

The equation of the curve passing through (2, 7/2) and having gradient 

A normal at any point (x, y) to the curve y = f(x) cuts a triangle of unit area with the axis, the differential equation of the curve is

The differential equation of all parabola each of which has a latus rectum 4a and whose axis parallel to the x-axis is