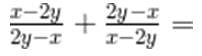Test: Problem Solving- 2 - CUET Commerce MCQ
10 Questions MCQ Test General Test Preparation for CUET - Test: Problem Solving- 2
A racecar driver has completed 12 1/2 laps of a 50 lap race. What fractional part of the race remains?
If M is the set of positive multiples of 2 less than 150 and N is the set of positive multiples of 9 less than 150, how many members are there in M n N?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
At Bruno’s Video World, the regular price for a DVD is d dollars. How many DVDs can be purchased for x dollars when the DVDs are on sale at 20% off the regular price?
If Dave drove one-third of the distance of his trip on the first day, and 60 miles on the second day, he figured out that he still had 1/2 of the trip to drive. What was the total length, in miles, of his trip?
Eddie is 7 years older than Brian. If Brian is x years old, then how old was Eddie 11 years ago?
Working alone at their respective constant rates, A can complete a task in ‘a’ days and B in ‘b’ days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task in exactly 10 days. If B starts, they take half a day more. How long does it take to complete the task if they both work together?
According to the graph below, the greatest change in the profit of the Sports Shack occurred between which two consecutive months?

If a, b, and c are not equal to zero, what is the difference between the maximum and minimum value of S? S
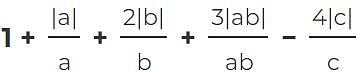
|
154 videos|396 docs|723 tests
|
|
154 videos|396 docs|723 tests
|