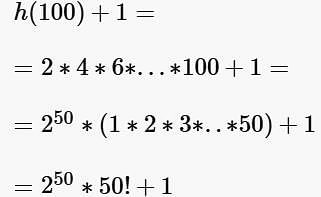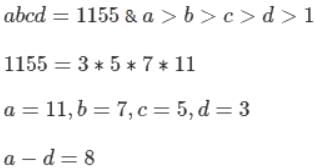Test: Factors And Multiples- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Factors And Multiples- 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Is integer y divisible by 24?
1) y is divisible by 6?
2) y is divisible by 4?
Is integer y divisible by 16?
1) y is divisible by 8
2) 2y is divisible by 16
Is integer y divisible by 16?
1) y2 is divisible by 16
2) y3 is divisible by 16
Integer x represents the product of all integers between 1 and 25, inclusive. The smallest prime factor of (x + 1) must be _____.
For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) +1, then p is?
Is x divisible by y?
1) (x – 1) is divisible by y
2) x > y
Is x divisible by y?
1) x is a multiple of (y + 1)
2) y > 1
If the product of the integers a, b, c, and d is 1155 and if a > b > c > d > 1, then what is the value of a – d?
What is the greatest common factor of positive integers x and y?
1) x and y share only one common factor. ?
2) x and y are unique prime numbers. ?
If 6x = 8y = 14z, then what is a possible sum of positive integers x, y, and z?
If 6x = 8y = 14z, then what is a possible sum of positive integers x, y, and z?
Which of the following CANNOT be the greatest common divisor of two positive integers a and b?
|
110 videos|110 docs|120 tests
|
|
110 videos|110 docs|120 tests
|