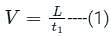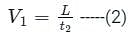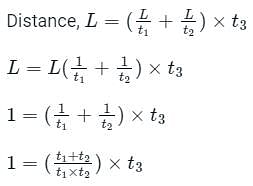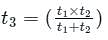Test: Relative Velocity in Two Dimensions - ACT MCQ
10 Questions MCQ Test Science for ACT - Test: Relative Velocity in Two Dimensions
A body is moving with a constant acceleration of 11î + 2ĵ, starting from î + ĵ. What will be the position of the body after 10s?
A body is moving with a constant velocity of 4î + 3ĵ, starting from the origin. What will be the position of the body after 10s?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Velocity of a man is 25 units in the positive X direction and 75 units in negative Y direction starting from the origin. Velocity of a woman is 25 units in the positive Y direction and 75 units in the negative X direction starting from the origin. What is the relative velocity of the man with respect to the woman?
The velocity of a car A is to 5î + 11ĵ. The velocity of another car B is 11î + 5ĵ. What is the relative velocity of B with respect to A?
A body is moving with a constant acceleration of 4î + 3ĵ, starting from the origin. What will be the position of the body after 5s?
Velocity of a dog is 15 units in the positive X direction and 3 units in positive Y direction starting from the origin. Velocity of a pig is 7 units in the positive Y direction and 17 units in the positive X direction starting from the origin. What is the relative velocity of the dog with respect to the pig?
The velocity of a car A is to 5î. The velocity of another car B is 22î – 7ĵ. What is the relative velocity of A with respect to B?
When two bodies move uniformly towards each other, the distance decrease by 6 m/s. If both the bodies moves (as above) in the same direction with the same speed, the distance between them increases by 4 m/s. Then the speed of the two bodies are
At a metro station, a girl walks up a stationary escalator in time t1 . If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be
If S = 3t2 - 5t + 7 find initial velocity.
|
486 videos|517 docs|337 tests
|