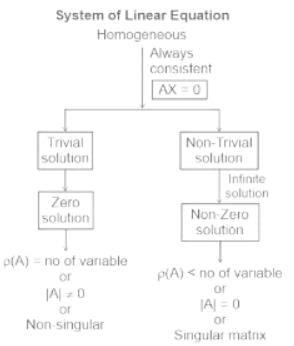
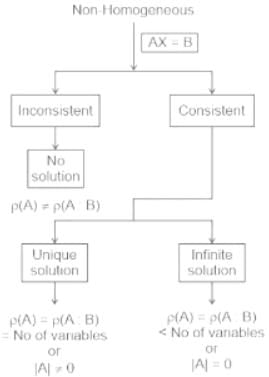
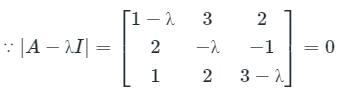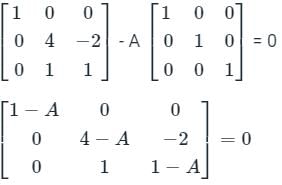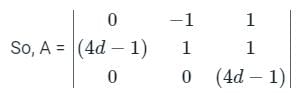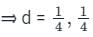Test: System of Linear Equations - ACT MCQ
15 Questions MCQ Test - Test: System of Linear Equations
If the system
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are
For what value of μ do the simultaneous equations 5x + 7y = 2, 15x + 21y = μ have no solution?
Gauss-Seidel method is used to solve the following equations (as per the given order):
x1 + 2x2 + 3x3 = 5
2x1 + 3x2 + x3 = 1
3x1 + 2x2 + x3 = 3
Assuming initial guess as x1 = x2 = x3 = 0, the value of x3 after the first iteration is ________
The value of k, for which the following system of linear equations has a non-trivial solution.
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0
For what value of λ, do the simultaneous equation 2x + 3y = 1, 4x + 6y = λ have infinite solutions?
For what value of k, the system linear equation has no solution
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0
The value of k for which the system of equations x + ky + 3z = 0, 4x + 3y + kz = 0, 2x + y + 2z = 0 has non-trivial solution is
Consider matrix 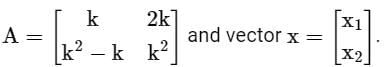 The number of distinct real values of k for which the equation Ax = 0 has infinitely many solution is________
The number of distinct real values of k for which the equation Ax = 0 has infinitely many solution is________
The set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =
Consider the system of equations 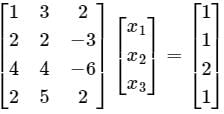 The value of x3 (round off to the nearest integer), is ______.
The value of x3 (round off to the nearest integer), is ______.
The approximate solution of the system of simultaneous equations
2x - 5y + 3z = 7
x + 4y - 2z = 3
2x + 3y + z = 2
by applying Gauss-Seidel method one time (using initial approximation as x - 0, y - 0, z - 0) will be:
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A?
Consider a matrix 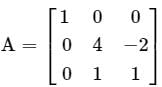
The matrix A satisfies the equation 6A-1 = A2 + cA + dI, where c and d are scalars and I is the identity matrix. Then (c + d) is equal to
The system of linear equations
-y + z = 0
(4d - 1) x + y + Z = 0
(4d - 1) z = 0
has a non-trivial solution, if d equals



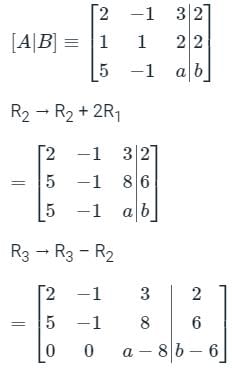
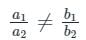
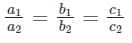
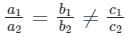
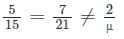


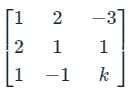
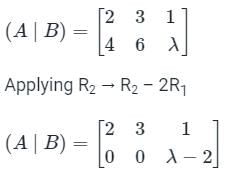
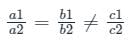
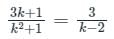

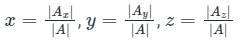
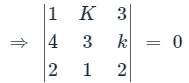




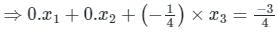
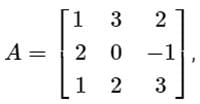 then which one of the following is correct?
then which one of the following is correct?