Test: Fractions/Ratios/Decimals - GMAT MCQ
10 Questions MCQ Test Practice Questions for GMAT - Test: Fractions/Ratios/Decimals
In a 200 member association consisting of men and women, exactly 20% of men and exactly 25 % women are homeowners. What is the least number of members who are homeowners?
A salad dressing requires oil, vinegar, and water in the ratio 2 : 1 : 3. If Oliver has 1 cup of oil, 1/3 cup of vinegar, and 2 cups of water, what is the maximum number of cups of dressing that he can mix?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two mixtures of X and Y have X and Y in the ratio 3:2 and 3:4. In what proportion should these two mixtures be mixed to get a new mixture in which the ration of X to Y is 5:4?
In a partnership, A invests 1/6 th of the capital for 1/6 th of the time, B invests 1/3 rd of the capital for 1/3 rd of the time and C invests the rest of the capital for the whole time. Out of a profit of $4140, A’s share is:
The ratio of boys to girls in the junior class is 2 to 3 respectively and the ratio of girls to boys in the senior class is 7 to 3 respectively. If there are 300 more students in the senior class than in the junior class and the combined ratio of boys to girls in both classes is 8 to 17 respectively, how many students are in the senior class?
Box A contains white, blue and red balls where the ratio of the number of white balls to the number of blue balls is 1:2 and the ratio of the number of blue balls to the number of red balls is 4:3. Box B contains white balls and blue balls in the ratio 4:5. Box C contains only blue balls so that the ratio of the number of blue balls in Box C to the number of white balls in Box A is 3:2. If the total number of blue balls in all the three boxes is 45, what is the number of white balls in Box B?
At a bakery, Tom normally earns x dollars per hour of the first n hours of the day. For each hour he works in excess of n hours on a given day, he is paid 1.375 times his regular rate. If Tom decides to start working over time, what is the ratio of over time hours to regular time hours required to double his daily income?
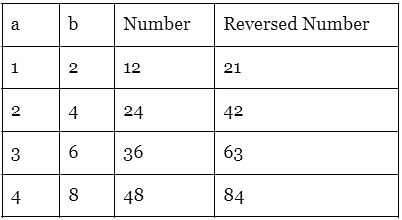
The ratio of a two digit number to a number formed by reversing its digits is 4:7. Which of the following is the sum of all the numbers of all such pairs?
If n is a positive integer, how many of the ten digits from 0 through 9 could be the units digits of n3 ?
A beaker was filled with a mixture of 40 liters of water and a liquid chemical. They are fixed in the ratio of 3 : 5, respectively. If 2 percent of the initial quantity of water and 5 percent of the initial quantity of liquid chemical evaporated each day during a 10-day period, what percent of the original amount of mixture evaporated during this period?
|
18 docs|139 tests
|