Test: Arithmetic - GMAT MCQ
10 Questions MCQ Test - Test: Arithmetic
X, Y and Z are positive integers, and X + 2Y + 2Z = 13. Z = ?
(1) X > Y > Z
(2) None of them is equal to 4
(2) None of them is equal to 4
Byrne and some of his friends go out to dinner and spend $111, excluding tax and tip. If the group included both men and women, how many men were in the group?
(1) There are a total of five people at the table, including Byrne.
(2) The women order meals that cost an average of $19 and the men order meals that cost and average of $27.
(2) The women order meals that cost an average of $19 and the men order meals that cost and average of $27.
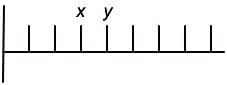
If the tick marks shown on the number line above are equally spaced and if x and y are the numbers designating the end points of an interval, as shown, what is the value of x?
(1) x = (3y)/4
(2) y = 2
If the tick marks shown on the number line above are equally spaced and if x and y are the numbers designating the end points of an interval, as shown, what is the value of x?
(2) y = 2
Is the sum of 7x and 7y divisible by 14?
(1) x = y
(2) x and y are both even integers
At least 10 cars have tinting window and fog light. 40% cars which have tinting windows also have fog light, is the number of the cars with tinting windows larger than that of the cars with the fog light?
(1) 80% cars which have fog light also have tinting windows
(2) 52 cars have tinting windows or fog light or both
If x, a 3-digit number, is sum of two 2-digit numbers, y and z, then what is y?
(1) The tens digit of x is one less than the tens digit of z.
(2) The sum of digits of y is equal to the tens digit of y.
Both a, b, and c are 3-digits integers, where a=b+c. Is the hundreds' digit of number a equal to sum of that of b and c?
(1) Tens' digit of a=tens' digit of b+tens' digit of c
(2) Units' digit of a=units' digit of b+units' digit of c
The sum of the elements in set A is 700. Is the the number of elements in set A less than 6?
(1) The average (arithmetic mean) of the greatest 3 elements is 150
(2) No elements of set A are less than 125
How many of the numbers x, y, and z are positive if each of these numbers is less than 10?
(1) x + y + z = 20
(2) x + y = 14
Mrs. K is paid at a reduced rate for contracts completed late, and the contract prices may vary. Her compensation for the first two late contracts in any month is reduced by 10%, and her compensation for any subsequent late contracts in the same month is reduced by 15%. If Mrs. K completed three contracts late, in the same month, was her total compensation for those three contracts reduced by more than 11%?
(1) Without any reduction, she would have received $550 for the last of the three late contracts, and at least $1200 for each of the others.
(2) Without any reduction, she would have received $1500 for the first of the three late contracts.














