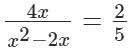Test: Algebra - GMAT MCQ
10 Questions MCQ Test - Test: Algebra
What is the absolute difference between the cubes of two different non-negative integers?
(1) One of the integers is 2 greater than the other integer.
(2) The square of the sum of the integers is 49 greater than the product of the integers.
(2) The square of the sum of the integers is 49 greater than the product of the integers.
a, b, and c are three distinct positive integers. What is the product abc?
(1) a + b + c = 7
(2) ab + bc + ca = 14
(2) ab + bc + ca = 14
If integer k > 0 and x2 − 7x + k = 0, what is the value of k?
(1) Both roots are prime number
(2) 2 is one of root of the equation
The revenue R, in dollars, that is generated by selling “x” units of a certain product is given by 9x2 + bx + c, where x > 0 and b and c are constants. Find the value of b.
(1) The revenue generated by selling 200 units of the product is 54,0000.
(2) The roots of the equation ax2 - bx + c are 20 and 9.
If x and y are positive integers and y = 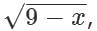 what is the value of y?
what is the value of y?
(1) x < 8
(2) y > 1
What is the value of the integer n?
(1) n2 + 3n = 4
(2) (n + 3)n = 1
If the elevation above water level of a breaching wale is given by the expression −t2 + 12t − 35 where t is the time, in seconds, after an observer begins watching, is the whale presently underwater?
(1) t < 8.
(2) t > 5.
If x and y are integers such that x < y < 0 what is x - y ?
(1) (x + y)(x - y) = 5
(2) xy = 6