Mathematics Test - 2 - SAT MCQ
30 Questions MCQ Test Digital SAT Mock Test Series 2024 - Mathematics Test - 2
How many solutions to the equation 4 cos x = 1 lie between x = 0 and x = 3π
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the smallest positive integer value of x such that 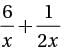 is less than 1?
is less than 1?
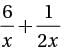 is less than 1?
is less than 1?
In the figure above, rectangle ABCD is inscribed in the circle with center O. What is the area of the circle?
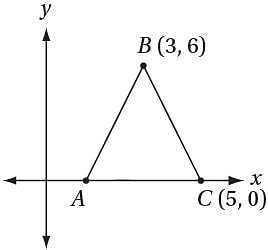
In the figure above, AB = BC. If 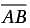 has a slope of m and
has a slope of m and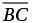 has a slope of n, what is the value of mn ?
has a slope of n, what is the value of mn ?
A total of 300 tickets were sold for a performance of a school play. The ticket prices were $5 for each adult and $3 for each child, and the total revenue from tickets was $1,400. Solving which of the following systems of equations would yield the number of adult tickets sold, a, and the number of children's tickets sold, c?
Which of the following equations represents a parabola in the xy-plane with a vertex that lies on the x-axis?
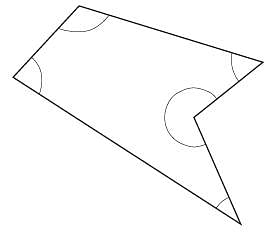
The figure above shows a polygon with five sides. What is the average (arithmetic mean) of the measures, in degrees, of the five angles shown?
The number of states that joined the United States between 1776 and 1849 is twice the number of states that joined between 1850 and 1900. If 30 states joined the United States between 1776 and 1849 and x states joined between 1850 and 1900, which of the following equations is true?
kx − 3y = 4
4x − 5y = 7
In the system of equations above, k is a constant and x and y are variables. For what value of k will the system of equations have no solution?
At a lunch stand, each hamburger has 50 more calories than each order of fries. If 2 hamburgers and 3 orders of fries have a total of 1700 calories, how many calories does a hamburger have?

The table above shows some values of the linear function f. Which of the following defines f ?
Graphene, which is used in the manufacture of integrated circuits, is so thin that a sheet weighing one ounce can cover up to 7 football fields. If a football field has an area of approximately 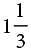 acres, about how many acres could 48 ounces of graphene cover?
acres, about how many acres could 48 ounces of graphene cover?
Mr. Kohl has a beaker containing n milliliters of solution to distribute to the students in his chemistry class. If he gives each student 3 milliliters of solution, he will have 5 milliliters left over. In order to give each student 4 milliliters of solution, he will need an additional 21 milliliters. How many students are in the class?
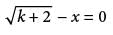
In the equation above, k is a constant. If x = 9, what is the value of k?
If a2 + b2 = z and ab = y, which of the following is equivalent to 4z + 8y?
Alan drives an average of 100 miles each week. His car can travel an average of 25 miles per gallon of gasoline. Alan would like to reduce his weekly expenditure on gasoline by $5. Assuming gasoline costs $4 per gallon, which equation can Alan use to determine how many fewer average miles, m, he should drive each week?
Intersecting lines r, s, and t are shown below.
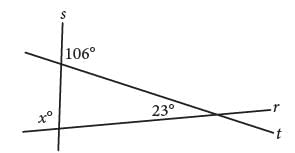
What is the value of x?
The weight of an object on Venus is approximately 9/10 of its weight on Earth. The weight of an object on Jupiter is approximately 23/10 of its weight on Earth. If an object weighs 100 pounds on Earth, approximately how many more pounds does it weigh on Jupiter than it weighs on Venus?
The density d of an object is found by dividing the mass m of the object by its volume V. Which of the following equations gives the mass m in terms of d and V?
A polling agency recently surveyed 1,000 adults who were selected at random from a large city and asked each of the adults, “Are you satisfied with the quality of air in the city?” Of those surveyed, 78 percent responded that they were satisfied with the quality of air in the city. Based on the results of the survey, which of the following statements must be true?
I. Of all adults in the city, 78 percent are satisfied with the quality of air in the city.
II. If another 1,000 adults selected at random from the city were surveyed, 78 percent of them would report they are satisfied with the quality of air in the city.
III. If 1,000 adults selected at random from a different city were surveyed, 78 percent of them would report they are satisfied with the quality of air in the city.
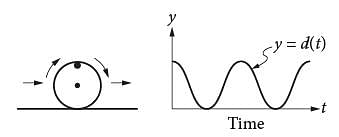
The figure on the left above shows a wheel with a mark on its rim. The wheel is rolling on the ground at a constant rate along a level straight path from a starting point to an ending point. The graph of y = d(t) on the right could represent which of the following as a function of time from when the wheel began to roll?
The expression 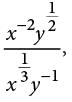 where x > 1 and y > 1,is equivalent to which of the following?
where x > 1 and y > 1,is equivalent to which of the following?
In the equation (αx + 3)2 = 36, a is a constant. If x = − 3 is one solution to the equation, what is a possible value of α?
A software company is selling a new game in a standard edition and a collector’s edition. The box for the standard edition has a volume of 20 cubic inches, and the box for the collector’s edition has a volume of 30 cubic inches. The company receives an order for 75 copies of the game, and the total volume of the order to be shipped is 1,870 cubic inches.Which of the following systems of equations can be used to determine the number of standard edition games, s, and collector’s edition games, c, that were ordered?
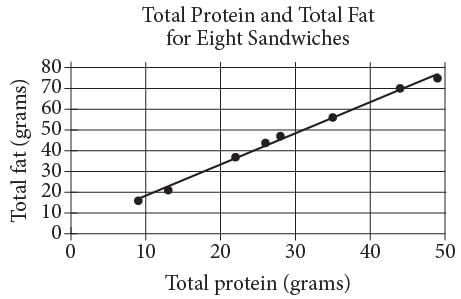
The scatterplot above shows the numbers of grams of both total protein and total fat for eight sandwiches on a restaurant menu. The line of best fit for the data is also shown. According to the line of best fit, which of the following is closest to the predicted increase in total fat, in grams, for every increase of 1 gram in total protein?
|
8 docs|15 tests
|


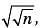 where n > 0, what is t he value of m in terms of n ?
where n > 0, what is t he value of m in terms of n ?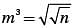
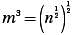
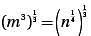
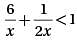
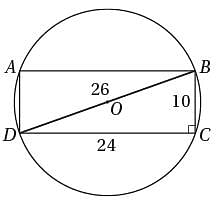
 and
and are opposites. We can calculate the slope of BC from its endpoints:
are opposites. We can calculate the slope of BC from its endpoints: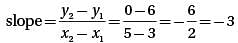
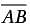 is 3, and so mn = (3)(-3) = -9.
is 3, and so mn = (3)(-3) = -9.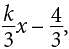 where k/3 is the slope of the line, and the equation 4x − 5y = 7 can be rewritten as y =
where k/3 is the slope of the line, and the equation 4x − 5y = 7 can be rewritten as y =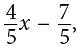 where 4/5 is the slope of the line. If two lines are parallel, then the slopes of the line are equal. Therefore, 4/5 = k/3, or k = 12/5. (Since the y-intercepts of the lines represented by the equations are
where 4/5 is the slope of the line. If two lines are parallel, then the slopes of the line are equal. Therefore, 4/5 = k/3, or k = 12/5. (Since the y-intercepts of the lines represented by the equations are 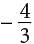 and
and 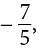 the lines are parallel, not identical.)
the lines are parallel, not identical.)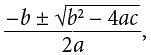 with α = 1, b = 4, and c = 2, gives the solutions x = −2 ± √2.
with α = 1, b = 4, and c = 2, gives the solutions x = −2 ± √2. acres, than 336 football fields have a total area of 336 ×
acres, than 336 football fields have a total area of 336 ×  = 448 acres. Therefore, of the choices given, 450 acres is closest to the number of acres 48 ounces of graphene could cover.
= 448 acres. Therefore, of the choices given, 450 acres is closest to the number of acres 48 ounces of graphene could cover. . Choice B is incorrect and may be the result of finding the number of football fields, not the number of acres, that can be covered by 48 ounces of graphene. Choice D is incorrect and may be the result of setting up the expression
. Choice B is incorrect and may be the result of finding the number of football fields, not the number of acres, that can be covered by 48 ounces of graphene. Choice D is incorrect and may be the result of setting up the expression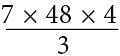 and then finding only the numerator of the fraction.
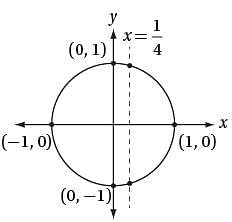
and then finding only the numerator of the fraction.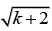 - x = 0, this equation becomes
- x = 0, this equation becomes  - 9 = 0, which can be rewritten as
- 9 = 0, which can be rewritten as 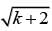 = 9 . Squaring each side of
= 9 . Squaring each side of 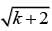 = 9 gives
= 9 gives 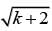 = 81, or k = 79. Substituting k = 79 into the equation
= 81, or k = 79. Substituting k = 79 into the equation 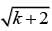 - 9 = 0 confirms this is the correct value for k.
- 9 = 0 confirms this is the correct value for k.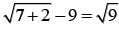 - 9 = 3 - 9 = 0, which is false.
- 9 = 3 - 9 = 0, which is false.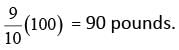 The same object’s weight on Jupiter is approximately 23/10 of its weight on Earth; therefore, the object weighs
The same object’s weight on Jupiter is approximately 23/10 of its weight on Earth; therefore, the object weighs 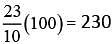 pounds on Jupiter. The difference between the object’s weight on Jupiter and the object’s weight on Venus is 230 − 90 = 140 pounds. Therefore, an object that weighs 100 pounds on Earth weighs 140 more pounds on Jupiter than it weighs on Venus.
pounds on Jupiter. The difference between the object’s weight on Jupiter and the object’s weight on Venus is 230 − 90 = 140 pounds. Therefore, an object that weighs 100 pounds on Earth weighs 140 more pounds on Jupiter than it weighs on Venus.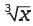 and √y, respectively. Also, x−2 and y-1 are equivalent to 1/x2 and 1/y , respectively. Using these equivalences, the given expression can be rewritten as
and √y, respectively. Also, x−2 and y-1 are equivalent to 1/x2 and 1/y , respectively. Using these equivalences, the given expression can be rewritten as 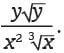
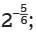 the values of the choices, however, are
the values of the choices, however, are 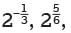 and 1, respectively.
and 1, respectively.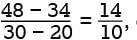 or 1.4. Of the choices given, 1.5 is the closest to the slope of the line of best fit.
or 1.4. Of the choices given, 1.5 is the closest to the slope of the line of best fit.














