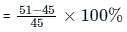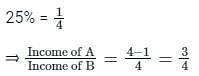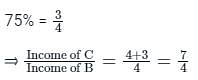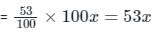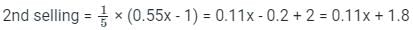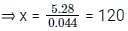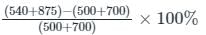Practice Test: Percentages- 2 - JAMB MCQ

Juice of 450 ml contains 5% fruit extract, 25% of pulp.

Amount of pulp = 450 × 25/100 = 112.5 ml

Now, let the amount of water added be ‘x’ ml.

Total volume of juice after adding water = 450 + x

New percentage of pulp = 15%

According to the question

⇒ (450 + x) × 15/100 = 112.5

⇒ (450 + x) = 750

∴ x = 300 ml

Given:

In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie

Formula used:

A got a% votes and B got b% votes, difference in the votes = (a - b) % of Total votes

Calculation:

Let the total votes be 100x

A Gets = 55x

B gets = 45x

Given that 10,000 votes of A given to B

As per question

⇒ 55x – 10,000 = 45x + 10,000

⇒ x = 2000

Total votes polled = 100x

⇒ 100 × 2000 = 200000

∴ Total votes polled is 200000

Given:

65% of a number is more than 25% of the number by 120.

Calculations:

Let the number be x

According to question, (65x/100) - (25x/100) = 120

⇒ (65x - 25x)/100 = 120

⇒ 40x/100 = 120

⇒ x = (120 × 100)/40 = 300

But we have to find 20%, so (20/100) × 300 = 60

∴ The required number is 60.

Shortcut Trick

65% - 25% = 120

⇒ 40% = 120

⇒ 20% = 60

∴ The required number is 60

Given:

Out of two numbers, 65% of the smaller number is equal to 45% of the larger

number. If the sum of two numbers is 2574

Calculation:

Let the smaller number be ‘x’ and the larger number be ‘y’

From the problem, it is given that

65%x = 45%y

⇒ 13x = 9y

⇒ x = (9/13)y    ----(1)

Given the sum of the numbers = 2574

⇒ (x + y) = 2574     ----(2)

Substituting the value of ‘x’ from Equation 1 in Equation 2, we get

(9/13)y + y = 2574

⇒ (9y + 13y) = 2574 × 13

⇒ 22y = (2574 × 13)

⇒ y = (2574 × 13)/22 = 1521

∴ Value of the larger number is 1521

Given:

Two students appeared for an examination. One of them secured 22

marks more than the other and his marks were 55% of the sum of

their marks

Calculation:

Let the students be A and B

Let the marks secured by B = x

Marks secured by A = x + 22

Sum of their marks of A & B = x + x + 22 = 2x + 22

Accoring to question, 

Marks of A =  55% of the sum of marks

⇒  x + 22 = 0.55 × (2x + 22) 

⇒ x + 22 = 1.1x + 12.1

⇒ 0.1x = 9.9

⇒ x = 9.9/0.1 = 99 marks

Marks secured by A = 99 + 22 = 121 marks

Therefore the correct answer is 121.

Shortcut Trick:

Let us go by options.

The difference between the numbers is 22 in all cases.

So, now check the next statement.

121 = 0.55 × (121+ 99) 

That is, as the first option itself satisfies the condition and since we do no have a combination of answers, it is the solution.

∴ The required numbers are 121 and 99.

Machine shows 20% less than the actual weight put on it, in some of the cases. So, Nathan gives more quantity than what he charges for. And hence he goes into loss.

The loss will be maximum when the wrong weight is shown with maximum probability, that is 0.6.

Let Nathan sells T kg in each transaction, and the cost price of T kg is C.

In 60% of total cases, amount Nathan will give = T/(1 – 20/100) kg = T/0.8 kg = 1.25T kg

In remaining 40% cases, Nathan gives T kg.

⇒ Average Amount given in a transaction = 0.6 × 1.25T + 0.4 × T = 1.15T

⇒ Cost price of a transaction = 1.15TC

And, selling price of a transaction = TC

We know, Selling Price = Cost Price × (1 - (Loss %)/100)

⇒ Loss Percentage = 100 × (1 – TC/1.15TC) = 13.04

∴ Maximum loss can be 13.04%.

Given:

Ted spends 55% of his income. His income increases by 28% and his expenditure also increases by 40%.

Concept used:

Income = Expenditure + Savings

Calculation:

Let the income of Ted be Rs. 100.

His expenditure = 100 × 55%

⇒ Rs. 55

His savings = 100 - 55

⇒ Rs. 45

Ted's increased income = 100 + 100 × 28%

⇒ Rs. 128

Ted's increased expenditure = 55 + 55 × 40%

⇒ Rs. 77

Ted's savings = 128 - 77

⇒ Rs. 51

Now, his savings increased by 

⇒ 13.3% (approx)

∴ The percentage of increase in his savings is 13.3%.

Given:

The income of A is 25% less than the income of B,

The income of C is 75% more than the income of B,

The difference in the income of A and C is Rs. 100.

Calculation:

Let 'x' be the income of B.

The income of A = (100% - 25%) of B = 75% of B

The income of C = (100% + 75%) of B = 175% of B

According to the question,

⇒ 175% of B - 75% of B = Rs. 100

⇒ 100% of B = Rs. 100

⇒ B = Rs. 100

Therefore, 'Rs. 100' is the required answer.

Alternate Method
The income of A is 25% less than the income of B,

The income of C is 75% more than the income of B,

In ratio form the above finding can be written as:

Income of A : Income of B : Income of C = 3 : 4 : 7 

According to the question,

⇒ 7k - 3k = 100

⇒ 4k = 100

⇒ k = 25

The income of B = 4k = Rs. 100

Therefore, 'Rs. 100' is the required answer.

Formula Used:

Mass percentage in solution = Total Salt/Total Solution × 100

Calculation:

Quantity of salt = 33g

Quantity of water = 320 g

The total quantity of solution,

⇒ 33 + 320 = 353 g

Now by using the formula,

Percentage of salt in the solution

⇒ (33/353) × 100 = 9.35% (approx)

∴ Mass percentage of the solution is 9.35 %.

Given:

There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of the total votes and won by 304 votes.

Concept used:

Percentage

Calculation:

Let the total number of voters be 100x

10% of voters did not vote 

Number of voters who vote = 100x - 10x = 90x

48 votes were found invalid

Valid votes = 90x - 48

Votes gained by the winning candidate 

Votes gained by the loosing candidate = 90x - 48 - 53x

⇒ 37x - 48

As per the question,

⇒ 53x - (37x - 48) = 304

⇒ 16x = 304 - 48

⇒ 16x = 256

⇒ x = 16

∴ Total number of voters = 100x = 1600

Alternate Method

Let total number of votes be 100 units,

10% voters did not cast their vote

⇒ Votes polled = 90 units

The winning candidate got 53% of all the voters in the list and won by 304 votes,

⇒ Winning candidate got = 53 units votes

⇒ Other candidate got = 37 units votes

⇒ Difference in votes = 53 units votes - 37 units votes = 304 - 48 = 256 votes

⇒ 16 units = 256

∴ 100 units votes = 256/16 × 100 = 1600 votes

∴ Total number of voters = 1600.

Given:

If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre

Calculation:

Let the consumption be 100 litres.

When price is Rs. 40 per litres, then, the expenditure = 100 × 40

⇒ Rs. 4,000.

At Rs. 60 per litre, the 60 × consumption = 4000

Consumption = 4,000/60 = 66.67 litres.

∴ Required decreased % = 100 - 66.67 = 33.33%

Given:

Average is 280.

Formula used:

Average = sum of the observation/number of the observation     

Calculation:

Let the number be x

According to the question,

⇒ (x + 50% of x + 25% of x)/3 = 280

⇒ (x + x/2 + x/4)/3 = 280

⇒ 7x/12 = 280

⇒ x =  480

∴ The number is 480.

Let the initial oranges with the fruit seller be x.

1st selling = 0.45x + 1

Remaining = x - (0.45x + 1) = 0.55x - 1

Remaining after second selling = 0.55x - 1 - (0.11x + 1.8) = 0.55x - 0.11x - 1 - 1.8 = 0.44x - 2.8

3rd selling = 90% × (0.44x - 2.8)

Remaining after 3rd selling = 0.1 × (0.44x - 2.8) = 0.044x - 0.28

According to the question-

⇒ 0.044x - 0.28 = 5

⇒ 0.044x = 5.28

∴ The number of oranges was 120. 

Given:

The income of Doyel is 40% more than that of Chitra.

Chitra got an 8% hike in his income, and Doyel got a 25% hike in her income.

Concept used:

Incremented/Reduced value = Initial value (1 ± change%)

Calculation:

Let the income of Chitra be Rs. 500.

Income of Doyel = 500 × 1.4

⇒ Rs. 700

Income of Chitra after the hike = 500 × (1 + 8/100)

⇒ Rs. 540

Income of Doyel after the hike = 700 × (1 + 25/100)

⇒ Rs. 875

Now, percentage increase in their income combined = 

⇒ 17.916% ≈ 18%

∴ The increase in their percentage combined income is 18%.

Given:

An engineering student has to secure 15% marks to pass.

A student gets 55 marks and fails by 20 marks.

Calculation:

Let the total marks be x

Passing marks = x × 15%

Passing marks = 15x/100      ----(1)

According to the question,

Passing marks = 55 + 20 = 75      ----(2)

From equation (1) and (2) we get,

⇒ 15x/100 = 75

⇒ x = 7500/15

⇒ x = 500

∴ The maximum marks of the student is 500.

Shortcut Trick

Passing percentage = 15%

Passing marks = 55 + 20 = 75

Maximum marks = (75/15) × 100 = 500

∴ The maximum marks of the student is 500.